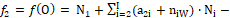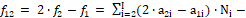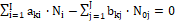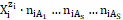Abstract
The Generalized Electron Balance (GEB) concept, related to electrolytic redox systems, is considered according to principles of Generalized Approach to Electrolytic Systems (GATES). Two equivalent Approaches (I and II) to GEB are presented. The Approach I, when perceived in convention of the card game, is based on the common pool of electrons as money, introduced by electron-active elements, named as players; electron-non-active elements are called there as fans. The GEB obtained according to Approach II results from the linear combination f12 = 2∙f(O) – f(H) of elemental balances: f1 = f(H) for H, and f2 = f(O) for O. Very important properties of f12 are presented here in details, and illustrated by a redox system where comproportion- ation reactions occur
Author Contributions
Academic Editor: Dr. Ashish Kumar, Associate Professor and HOD -Department of Chemistry, Lovely Professional University Phagwara, India.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2018 Anna M. Michałowska-Kaczmarczyk, et al.
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
The linear combination f12 = 2⋅f(O) – f(H) of elemental balances: f1 = f(H) for H, and f2 = f(O) for O, can be formulated for electrolytic redox and non-redox systems, of any degree of complexity, where charge (f0 = ChB) and elemental/core balances fk = f(Yk)for Yk ≠ H, O (k≥3, …, K) are also formulated, according to Generalized approach to redox systems (GATES) principles. The set of K independent balances f0, f12, f3, …, fK is necessary for thermodynamic resolution of a redox system; all the balances are presented here in the form fk = 0 (k = 0, …, K). A non-redox system is resolvable with use of K–1 independent balances f0, f3, …, fK. In a non-redox system, f12 is the dependent balance, indicated by the linear combination 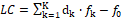 , where dk are the oxidation numbers (ONs) for Y1 = H, Y2 = O, and Yk (k≥3, …, K). For a non-redox system, the LC is expressed by identity, 0 = 0, i.e., f12 is linearly dependent on f0, f3, …, fK, and then
, where dk are the oxidation numbers (ONs) for Y1 = H, Y2 = O, and Yk (k≥3, …, K). For a non-redox system, the LC is expressed by identity, 0 = 0, i.e., f12 is linearly dependent on f0, f3, …, fK, and then  . For a redox system, LC is expressed by equation different from the identity, i.e., f12 is the new balance in the redox system. Therefore, the linear dependency/independency of f12 from f0, f3, …, fK is the general criterion distinguishing between non-redox and redox systems, of any degree of complexity.
. For a redox system, LC is expressed by equation different from the identity, i.e., f12 is the new balance in the redox system. Therefore, the linear dependency/independency of f12 from f0, f3, …, fK is the general criterion distinguishing between non-redox and redox systems, of any degree of complexity.
The Approach II to GEB (formulated 2005) was preceded by the Approach I to GEB (formulated 1992); both approaches are equivalent, i.e.,
Approach I to GEB ⟺ Approach II to GEB (1)
Formulation of GEB according to Approach I can be perceived in the convention of the card game, based on the common pool of electrons as money, introduced by electron-active elements, named as players; electron-non-active elements are called there as fans. In a redox system, the arranged set (f1, f2, …, fk, fk+1,, …, fK) of K balances f1, …, fK involves K* balances f1, f2, …, fk*, for fans, and K – K* balances fk*+1,…, fK for players. In a non-redox system we have K* = K fans, i.e., the number of players is K – K* = 0 in there; H and O are considered here as fans.
The prior knowledge of ONs for all elements of the system in question is not needed in the Approach II to GEB, contrary to the formulation of GEB according to Approach I, where the knowledge of ONs for players is required.
All the regularities indicated above will be confirmed in an example presented below, and illustrated graphically. Further generalizing comments will also be presented.
Redox Systems in Chemistry
In chemical laboratories, redox reactions are usually referred to processes occurred during redox titrations. Since redox reactions are so important class of chemical reactions, we should know their physicochemical nature thoroughly, from the titrimetric viewpoint.
Titration is considered as a kind of dynamic process, where V mL of titrant T is added, from the start, up to a given point of the titration, into V0 mL of titrand D, and V0 + V mL of D+T mixture is obtained, if the volumes additivity is valid/tolerable. The species formed in the D+T systems are involved in the related balances.
In aqueous media, the species 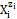 exist as hydrates
exist as hydrates 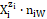 zi = 0, ±1, ±2, … is a charge, expressed in terms of elementary charge units, e = F/NA (F = 96485 C∙mol−1 – Faraday’s constant, NA = 6.022∙1023 mol-1 – Avogadro’s number), ni = niW ≥ 0 is a mean number of water (W=H2O) molecules attached to
zi = 0, ±1, ±2, … is a charge, expressed in terms of elementary charge units, e = F/NA (F = 96485 C∙mol−1 – Faraday’s constant, NA = 6.022∙1023 mol-1 – Avogadro’s number), ni = niW ≥ 0 is a mean number of water (W=H2O) molecules attached to 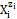 ;the case niW = 0 is then also admitted. For ordering purposes we assume:
;the case niW = 0 is then also admitted. For ordering purposes we assume: 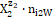 = H+1∙n2W,
= H+1∙n2W, 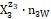 = OH-1∙n3W, i.e., z2 = +1, z3 = –1, … . Molar concentration of the species
= OH-1∙n3W, i.e., z2 = +1, z3 = –1, … . Molar concentration of the species  is denoted as
is denoted as 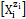 ;for a static system (volume V0 mL), we have
;for a static system (volume V0 mL), we have
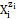 = 103∙(Ni/NA)/V0 (2)
= 103∙(Ni/NA)/V0 (2)
and for a dynamic D+T system
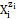 = 103∙(Ni/NA)/(V0+V). (2a)
= 103∙(Ni/NA)/(V0+V). (2a)
It is advisable to start the balancing from the interrelations between numbers of particular entities: N0j for components represented by molecules composing D and T, and Ni – for species 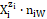 (ions and molecules) of i-th kind (i = 1, …, I), where I is the number of kinds of the species in the D+T. The mono- or two-phase electrolytic D+T system thus obtained involves N1 molecules of H2O and Ni species of i-th kind,
(ions and molecules) of i-th kind (i = 1, …, I), where I is the number of kinds of the species in the D+T. The mono- or two-phase electrolytic D+T system thus obtained involves N1 molecules of H2O and Ni species of i-th kind, 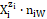 (i = 2, 3, …, I), specified briefly as
(i = 2, 3, …, I), specified briefly as 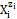 (Ni, ni), where ni ≡ niW ≡ niH2O is the mean number of hydrating water molecules (W=H2O) attached to
(Ni, ni), where ni ≡ niW ≡ niH2O is the mean number of hydrating water molecules (W=H2O) attached to 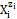 The net charge of
The net charge of 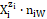 equals to the charge of
equals to the charge of 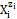 zi+ niW⋅0 = zi. For ordering purposes, we write the sequence: H+1 (N2, n2), OH-1 (N3, n3), … , i.e., z2 = 1, z3 = –1,.
zi+ niW⋅0 = zi. For ordering purposes, we write the sequence: H+1 (N2, n2), OH-1 (N3, n3), … , i.e., z2 = 1, z3 = –1,.
In the notation applied here, N0j (j =1, 2, …, J) is the number of molecules of the component of j-th kind, including water, forming D in static (V=0), or D and T in a dynamic D+T system. The D+T system thus obtained involves N1 molecules of H2O = ( 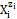 H2O, z1=0) and Ni species of i-th kind, (i = 2, 3, …, I), denoted briefly as
H2O, z1=0) and Ni species of i-th kind, (i = 2, 3, …, I), denoted briefly as 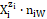 where ni≡ niW ≡ niH2O. The ni = niW values are virtually unknown – even for
where ni≡ niW ≡ niH2O. The ni = niW values are virtually unknown – even for 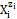 = H+1 1 in aqueous media, and depend on ionic strength (I) of the solution.
= H+1 1 in aqueous media, and depend on ionic strength (I) of the solution.
Electrolytic (redox and non-redox) systems are formulated according to the GATES principles 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40. For this purpose, the set of K+1 balances f0, f1, f2, f3, …, fK is obtained. The charged/ionic species of the system are involved in the charge balance
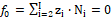 (3)
(3)
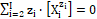 (3a)
(3a)
applicable for static and dynamic systems. Note that 0∙∙(xm) = 0 for a species  with zero charge (zm=0), e.g., 0∙[H2O] = 0 (z1=0).
with zero charge (zm=0), e.g., 0∙[H2O] = 0 (z1=0).
Free water particles (N1), and water bound in the hydrates  , are included in the balances: f1 = f(H) and f2 = f(O):
, are included in the balances: f1 = f(H) and f2 = f(O):
(4)
(5)
Next, the linear combination
 (6)
(6)
is obtained, where aki and bkj in equations 4-6 are the numbers of atoms/cores Yk (k = 1,...,K) in 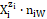 , and in the j-th component of the system, resp. The core is perceived as a non-transformable cluster of atoms, of the same elemental composition (expressed by chemical formula) and structure; e.g. the set of species: HSO4-1, SO4-2 and Fe SO4 contains SO4-2 as the core. One can notice that: (a) N1 involved with H2O as the species, (b) all N0i related to water as the component of the system, and (c) all ni = niW specified in f(H) and f(O) are cancelled within 2∙f(O) – f(H) in aqueous media. The necessity of prior knowledge of niW values in the balancing procedure is thus avoided. All these regularities are valid for non-redox and redox systems.
, and in the j-th component of the system, resp. The core is perceived as a non-transformable cluster of atoms, of the same elemental composition (expressed by chemical formula) and structure; e.g. the set of species: HSO4-1, SO4-2 and Fe SO4 contains SO4-2 as the core. One can notice that: (a) N1 involved with H2O as the species, (b) all N0i related to water as the component of the system, and (c) all ni = niW specified in f(H) and f(O) are cancelled within 2∙f(O) – f(H) in aqueous media. The necessity of prior knowledge of niW values in the balancing procedure is thus avoided. All these regularities are valid for non-redox and redox systems.
The elemental/core balances: f3, ..., fK, interrelating the numbers of atoms/cores Yk ≠ H, O in components and species, are as follows
fk = f(Yk) =
(k = 3, ..., K) (7)
All the balances f0, …, fK are presented here are as equations fk = 0, see equations 3–7.
In further parts of this paper, we concern on the procedure known in elementary algebra as linear combination 19, 41, in accordance with Noether's conceptual approach to linear algebra 42, 43. For this purpose, we consider first an example of titration in a redox system, where comproportionation 44 reactions occur. The conclusions arising in the formulation of this system (denoted as the system S, for brevity) will then be generalized later in discussion.
System S: KBrO3 (C) ⇒NaBr (C0) + H2SO4 (C01)
Let us consider the system, where V0 mL of Dis composed of NaBr (N01 molecules) + H2 SO4 (N02 molecules) + H2O (N03 molecules), and V mL of T is composed of KBrO3 (N04 molecules) + H2O (N05 molecules). The D+T mixture thus formed involves the following species:
H2O (N1), H+1 (N2,n2), OH-1 (N3,n3), HBrO3 (N4,n4),s, BrO3-1 (N5,n5), HBrO (N6,n6), BrO-1 (N7,n7),
Br2 (N8,n8), Br3-1 (N9,n9), Br-1 (N10,n10), Na+1 (N11,n11) , K+1 (N12,n12),
HSO4-1 (N13,n13), SO4-2 (N14,n14).
The Approach II to the System S
Denoting C0V0 = 103∙N01/NA, C01V0 = 103∙N02/NA, CV = 103∙N04/NA, we formulate the fraction titrated 16, 25, 45
Φ =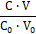 (8)
(8)
It provides a kind of normalization in the related graphs, i.e., independency on V0 value. The balances are as follows:
f0 = ChB :
N2 – N3 – N5 – N7 – N9 – N10 + N11 + N12 –
N13 – 2N14 = 0 ⟹ (9)
[H+1] – [OH-1] – [BrO3-1] – [BrO-1] – [Br3-1] – [Br-1] + [Na+1] + [K+1]
– [HSO4-1] – 2[SO4-2] = 0 (9a)
f1 = f(H) :
2N1 + N2(1+2n2) + N3(1+2n3) + N4(1+2n4) + 2N5n5 + N6(1+2n6) + 2N7n7 + 2N8n8 + 2N9n9 + 2N10n10 + 2N11n11 + 2N12n12 + N13(1+2n13) + 2N14n14 = 2N02 + 2N03 + 2N05
f2 = f(O) :
N1 + N2(1+n2) + N3(1+n3) + N4(3+n4) +
N5(3+n5) + N6(1+n6) + N7(1+n7) + N8n8 +
N9n9 + N10n10 + N11n11 + N12n12 + N13(4+n13) +
N14(4+n14) = 4N02 + N03 + 3N04 + N05
–f3 = –f(Na) :
N01 = N11 ⟹ [Na+1] = C0V0/(V0+V) (10)
–f4 = –f(K) :
N04 = N12 ⟹ [K+1] = CV/(V0+V) (11)
–f5 = –f(SO4) ⟺ –f5 = –f(S): (12)
N02 = N13 + N14 ⟹ (12a)
[H SO4-1] + [SO4-2] = C01V0/(V0+V) (12b)
f6 = f(Br) : N4 + N5 + N6 + N7 + 2N8 + 3N9 + N10
= N01 + N04 ⟹ (13)
[HBrO3] + [BrO3-1] + [HBrO] + [BrO-1] +2[Br2] +
3[Br3-1] + [Br-1] = (C0V0 + CV)/(V0+V) (13a)
f12 = 2 f(O) – f(H)
– N2 + N3 + 5N4 + 6N5 + N6 + 2N7 + 7N13 + 8N14
= 6N02 + 6N04 (14)
– [H+1] + [OH-1] + 5[HBrO3] + 6[BrO3-1] + [HBrO] + 2[BrO-1] + 7[HSO4-1] + 8[SO4-2]
= 6(C01V0 + CV)/(V0+V) (14a)
f12 + f0 – f3 – f4 – 6∙f5 = 0 ⟺ (+1)f1 +
(–2)f2 + (+1)f3 + (+1)f4 + (+6)f5 – f0 = 0 ⟺
(+1)f(H) + (–2)f(O) + (+1)f(Na) + (+1)f(K) +
(+6)f(S) – ChB = 0 (15)
5(N4+N5) + 1(N6+N7) – N9 – N10
= – N01 + 5N04 ⟹ (15a)
5([HBrO3] + [BrO3-1]) + [HBrO] + [BrO-1] –
[Br3-1] – [Br-1] =  + 5∙
+ 5∙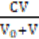 (15b)
(15b)
(+5)([HBrO3]+[BrO3-1]) + (+1)([HBrO]+[BrO-1]) + 2∙0∙[Br2] + 3∙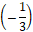 ∙[Br3-1] + (–1)[Br-1]
∙[Br3-1] + (–1)[Br-1]
= (–1)∙ 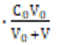 + (+5)∙
+ (+5)∙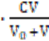 (15c)
(15c)
ZBr∙f6 – (f12 + f0 – f3 – f4 – 6∙f5)
(ZBr–5)(N4+N5) + (ZBr–1)(N6+N7) + 2ZBrN8 + (3ZBr+1)N9 + (ZBr+1)N10
= (ZBr+1)N01 + (ZBr–5)N04 ⟹ (16)
(ZBr–5)([HBrO3]+[BrO3-1]) + (ZBr–1(HBrO +[BrO-1]) + 2ZBr[Br2] + (3ZBr+1)[Br3-1] + (ZBr+1)[Br-1] =
(ZBr+1) 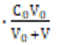 + (ZBr–5)∙
+ (ZBr–5)∙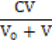 (16a)
(16a)
Other linear combinations are also possible. From the linear combination (f12 + f0 – f3 – f4 – 6∙f5 + f6)/2 we get the shortest (involving the smallest number of components) form of GEB for the system S:
3(N4+N5) + (N6+N7) + N8 + N9 = 3N04 (17)
3([HBrO3] + [BrO3-1]) + ([HBrO] + [BrO-1]) + [Br2] +
[Br3-1] = 3∙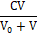 (17a)
(17a)
Note that the coefficients in eq. 15c are equal tothe oxidation numbers (ONs) of the elements considered as ‘fans’ in the system S, i.e., H, O, Na, K, S. Eq. 15b obtained from the combination 15 interrelates components and species formed by Br, as the player.
Other linear combinations a1∙f0 + a2∙f12 + 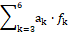 of the balances: f0, f12, f3, …, f6 are also acceptable, ak ∈ ℝ.
of the balances: f0, f12, f3, …, f6 are also acceptable, ak ∈ ℝ.
Equations 14a, 15b, 16a and 17a are alternative/equivalent equations for GEB related to the system S. One of the equations for GEB, together with equations 9a, 12b and 13a, form a complete set of equations related to the system S. The relations 10 and 11, considered as equalities (not equations), can be immediately introduced into eq. 9a as numbers.
In eq. 12b, the SO4-2 can be perceived as the core. However, because the system S has no other competing sulfate forms, the choice between f(S) and f(SO4) (eq. 12) is irrelevant.
Separate Approaches to D and T of the System S
We can also formulate the balances for D and T, considered separately, as independent units. Applying the notation specified above, we have:
for D :
f0 = ChB : N2 – N3 – N10 + N11 – N13 – 2N14 = 0
f1 = f(H) : 2N1 + N2(1+2n2) + N3(1+2n3) +
2N11n11 + N13(1+2n13) + 2N14n14 = 2N02 + 2N03
f2 = f(O) : N1 + N2n2 + N3(1+n3) + N11n11 +
N13(4+n13) + N14(4+n14) = 4N02 + N03
–f3 = –f(Na) : N01 = N11
–f5 = –f(SO4) : N02 = N13 + N14
f6 = f(Br) : N10 = N01
and then:
f12 = 2∙f2 – f1 : – N2 + N3 + 7N13 + 8N14 = 6N02
f12 + f0 – f3 – 6f5 + f6 = 0 ⟺ (+1)f(H) + (–2)f(O) + (+1)f(Na) + (+6)f(S) + (–1)f(Br) – ChB = 0 (18)
0 = 0 (18a)
for T :
f0 = ChB : N2 – N3 – N5 + N12 = 0
f1 = f(H) : 2N1 + N2(1+2n2) + N3(1+2n3) +
N4(1+2n4) + 2N5n5 + 2N12n12 = 2N05
f2 = f(O) : N1 + N2n2 + N3(1+n3) + N4(3+n4) +
N5(3+n5) + N12n12 = 3N04 + N05
–f4 = –f(K) :N04 = N12
–f6 = –f(Br) :N04 = N4 + N5
and then:
f12 = 2∙f2 – f1 : – N2 + N3 + 5N4 + 6N5 + 8N14 = 6N04
f12 + f0 – f4 – 5f6 = 0 ⟺ (+1)f(H) + (–2)f(O) + (+1)f(K) + (+5)f(Br) – ChB = 0 (19)
0 = 0 (19a)
The D and T, considered separately, form non-redox-systems; ONs for Br are: –1 in NaBr, and +5 in KBrO3, i.e., there are the boundary values of ONs in bromine redox systems; Br(+7) species are omitted in considerations 24.
The relations 0 = 0, named as identities, mean here that:
f12 is linearly dependent on: f0, f3, f5 and f6 in eq. 18, i.e., f12 = f3 + 6f5 – f6 – f0;
f12 is linearly dependent on: f0, f4 and f6 in eq. 19, i.e., f12 = f4 + 5f6 –f0.
In other words, the f12 are not the independent equations in D and T, considered here as separate subsystems.
Approach I to GEB in the System S
Unlike the Approach II exemplified above, the Approach I to GEB needs prior knowledge of ONs for all elements in components and species of the system in question. In the system S, there are K* = 5 ‘fans’, whereas bromine (Br) is considered as the ‘player, K – K* = 6 – 5 = 1 is here the number of players.
In the system S, bromine (as NaBr and KBrO3) is the carrier/distributor of the player electrons. One atom of Br has ZBr bromine electrons, and then one molecule of NaBr has ZBr +1 bromine electrons, one molecule of KBrO3 has ZBr–5 bromine electrons; then N01 molecules of NaBr involve (ZBr + 1)∙N01 bromine electrons, N04 molecules of KBrO3 involve (ZBr –5)N04 bromine electrons. Thus, the total number of bromine electrons introduced by NaBr and KBrO3 is (ZBr + 1)∙N01 + (ZBr – 5)N04. On this basis, we state that 2, 27:
N4 species HBrO3∙n4H2O involve (ZBr – 5)∙N4 bromine electrons;
N5 species BrO3-1∙n5H2O involve (ZBr–5)∙N5 bromine electrons;
N6 species HBrO∙n6H2O involve (ZBr–1)∙N6 bromine
electrons;
N7 species BrO-1∙n7H2O involve (ZBr–1)∙N7 bromine
electrons;
N8 species Br2∙n8H2O involve 2ZBr∙N8 bromine
electrons;
N9 species Br3-1∙n9H2O involve (3ZBr+1)∙N9 bromine
electrons;
N10 species Br-1∙n10H2O involve (ZBr+1)∙N10 bromine electrons.
The balance for the bromine electrons is then expressed by eq. 16 and then by eq. 16a. This confirms the equivalency of the Approaches I and II to GEB (eq. 1).
As stated above, the Approach I to GEB is compared to the ‘card game’ 27 (pp. 41-43), and – nominally – all electrons of the players are involved in the balance 16a. Following this line of reasoning, it can be also stated that the card players do not engage, as a rule, all their cash resources in the game. What's more – the ‘debt of honour’ principle can be applied 27 (p. 43). Simply, on the ground of linear combination, in eq. 16a one can replace ZBr for Br by ζBr ≠ ZBr; in particular, one can apply ζBr = 0, see equations 15a and 15b in context with equations 16 and 16a.
Computer Program for the System S
function F = Function_NaBr_H2 SO4_KBrO3(x)
%NaBr (C0) H2 SO4 (C01) V0 KBrO3 (C) V
global V Vmin Vstep Vmax V0 C C0 C01 fi H OH pH E Kw pKw A
global Br Br2 Br3 HBrO BrO HBrO3 BrO3 Na K H SO4 SO4
global logBr logBr2 logBr3 logHBrO logBrO logHBrO3 logBrO3
global logNa logK logH SO4 log SO4
E=x(1);
pH=x(2);
Br=10.^-x(3);
SO4=10.^-x(4);
H=10.^-pH;
pKw=14;
Kw=10.^-14;
OH=Kw./H;
A=16.9;
ZBr=35;
BrO3=Br.*10.^(6.*A.*(E-1.45)+6.*pH);
HBrO3=10.^0.7.*H.*BrO3;
BrO=Br.*10.^(2.*A.*(E-0.76)+2.*pH-2.*pKw);
HBrO=10.^8.6.*H.*BrO;
Br3=Br.^3.*10.^(2.*A.*(E-1.05));
Br2=Br.^2.*10.^(2.*A.*(E-1.087));
Na=C0.*V0./(V0+V);
K=C.*V./(V0+V);
%Charge balance
F=[(H-OH-BrO3-BrO-Br3-Br+Na+K- HSO4-2.* SO4);
%Concentration balance of Br
(HBrO3+BrO3+HBrO+BrO+2.*Br2+3.*Br3+
Br-(C0.*V0.+C.*V)/(V0+V));
%Concentration balance for SO4
(H SO4+2.* SO4-C01.*V0/(V0+V));
%GEB
((ZBr-5).*(HBrO3+BrO3)+(ZBr-1).*(HBrO+BrO)+2.*ZBr.*Br2...
+(3.*ZBr+1).*Br3+(ZBr+1).*Br...
-((ZBr+1).*C0.*V0+(ZBr-5).*C.*V)./(V0+V))];
logBr=log10(Br);
logBr2=log10(Br2);
logBr3=log10(Br3);
logHBrO=log10(HBrO);
logBrO=log10(BrO);
logHBrO3=log10(HBrO3);
logBrO3=log10(BrO3);
logH SO4=log10(H SO4);
log SO4=log10(SO4);
logNa=log10(Na);
logK=log10(K);
Graphical Presentation of Results for the System S
In the algorithm, prepared according to MATLAB computational software, the potential E V was expressed in SHE scale 46, pH = – log[H+1], , pBr = – log[Br-1], V0 = 100, C0 = 0.01, C = 0.1, C01 = 0, 0.01 or 0.1. The equilibrium constants related to this system were cited in ref. 2.
The results of calculations are presented graphically (Figure 1), as the graphs: (a) E = E(Φ), (b) pH = pH(Φ) and (c) speciation curves [ 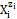 ] = φi(Φ), with the fraction titrated Φ (eq. 8) on the abscissas. The impact of growth in C01 concentration is illustrated here.
] = φi(Φ), with the fraction titrated Φ (eq. 8) on the abscissas. The impact of growth in C01 concentration is illustrated here.
At C01 = 0, comproportionation practically does not occur (IIIa); concentration of HBrO, as the major product formed in the comprortionation reaction
BrO3-1 + 2Br-1 + 3H+1 = 3HBrO sss (20)
is ca. 10-6 mol/L. The potential E increases monotonically (Figure. Ia), whereas pH first increases, passes through maximum and then decreases, see IIa). The relevant E and pH changes are small (Figures Ia, IIa). Binding the H+1 ions in reaction 21 causes a weakly alkaline reaction (Figure. IIa).
At C01 = 0.01 (Figures Ib, IIb, IIIb) and 0.1 (Figures Ic, IIc, IIIc), the stoichiometry 1 : 5, i.e., Φ eq = 0.2, see 16, 28, resulting from the shape of the related graphs, is expressed by reaction
BrO3-1 + 5Br-1 + 6H+1 = 3Br2 + 3H2O (21)
For Φ > 0.2, an increase of efficiency of the competing reaction 21 is noted. A growth of C01 value causes a small extension of the potential range in the jump region, on the side of higher E-values ((Figure 1, column I). With an increase of the C01 value, the graphs of pH vs. Φ resemble two almost straight line segments intersecting at Φ eq = 0.2 ((Figure 2, column II). However, the pH-ranges covered by the titration curves are gradually narrowed; it is an effect in growth of dynamic buffer capacity of the related redox systems 32.
Figure 1.The functions: E = E(Φ) (column I), pH = pH(Φ) (column II) and speciation diagrams (column III), at (C0,V0,C) = (0.01,100,0.1), and three different C01 values, indicated at the graphs.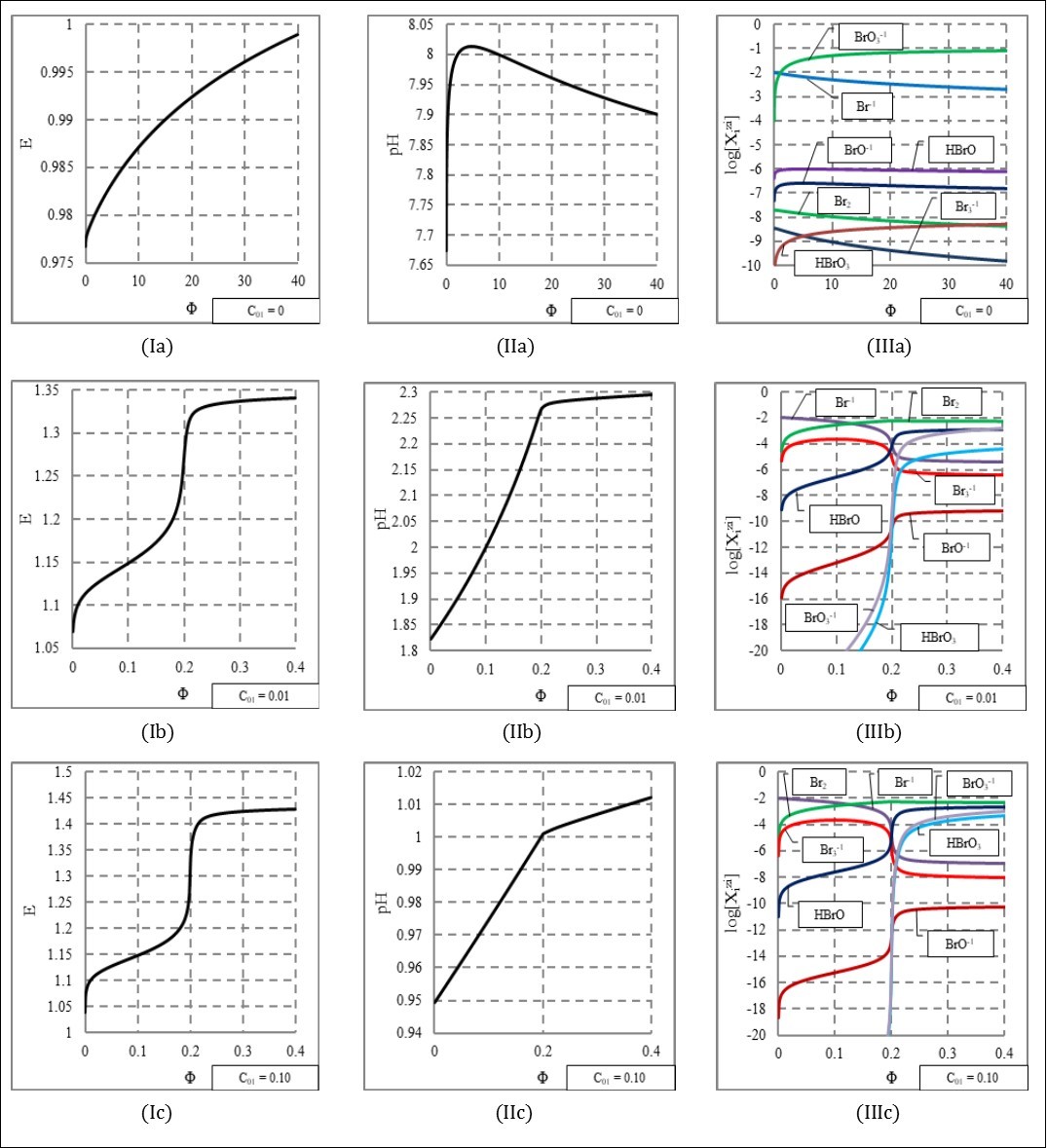
Concluding remarks
The linear combination
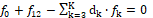 ⟺
⟺
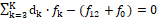 ⟺
⟺
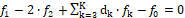 ⟺
⟺
 (22)
(22)
involves K balances: f0, f12, f3,…,fK where d1 = +1, d2 = –2. All the balances are presented here as equations, fk = 0.
In a non-redox system, we have K fans, i.e., the number of players equals zero. In a redox system, we have K* fans, K* < K, i.e., the number of players equals K – K* ( > 0).
When the multipliers dk are equal to (or involved with) the oxidation numbers (ONs) of the corresponding elements (k = 1, …, K) in a non-redox system, then eq. 22 is transformed into identity, 0 = 0. This proves that f12 is not the independent equation in the f0, f12, f3, …, fK, and  Then f0, f3, …, fK is the set of K–1 independent balances, composed of charge balance (f0) and K–2 elemental/core balances f3, …, fK.
Then f0, f3, …, fK is the set of K–1 independent balances, composed of charge balance (f0) and K–2 elemental/core balances f3, …, fK.
Referring now to a redox system, we arrange the elemental/core balances in the sequence f1, f2, …, fK*, fK*+1 , fK , and then formulate the equation
 (23)
(23)
involving the balances for K* electron-non-active elements, compare with equations 15, 18, 19.
If dk (k=1,…,K*) are equal to (or involved with) ONs of electron-non-active elements, then the resulting balance involves only the components (Ni, N0j) related to electron-active species/compounds, with coefficients equal to (or involved with) ONs of these element. More precisely, dk are the products of the number λk of defined atoms in the species and the ON value ωk, i.e.  (k = 1,…,K*). It is clearly visible in the case of Br3-1 in eq. 15c, where –1 = 3
(k = 1,…,K*). It is clearly visible in the case of Br3-1 in eq. 15c, where –1 = 3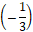 , and (less visible) in the case of Br2 in the eq. 15c, where 0 = 2∙0, i.e., the coefficient d9 = –1 at [Br3-1] in eq. 15b is involved with (not equal to) the oxidation number ω9 =
, and (less visible) in the case of Br2 in the eq. 15c, where 0 = 2∙0, i.e., the coefficient d9 = –1 at [Br3-1] in eq. 15b is involved with (not equal to) the oxidation number ω9 = 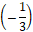 of bromine in Br3-1 (λ9 = 3).
of bromine in Br3-1 (λ9 = 3).
The equivalent relations were applied:
fk =  ⟺
⟺

(24)
for elements with negative oxidation numbers, or
-fk = 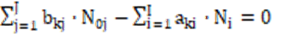 ⟺
⟺
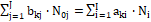
(25)
for elements with positive oxidation numbers, k ∈ 3, …,K. The change of places of numbers Ni for components and N0j for species at the equality sign in relations 24, 25 were made in order to avoid possible/simple mistakes in the realization of the linear combination procedure. This facilitates the purposeful linear combination of the balances, and enables to avoid simple mistakes in this operation. Note, for example, that f4 = f(Na) ⟺ f(Na) = f4 ⟺ –f4 = –f(Na).
Starting from K+1 balances: f0, f1, f2, f3, …, fK,, after formulation of the linear combination f12 we obtain the set of K balances: f0, f12, f3, …, fK,. In a non-redox system, f12 is the dependent balance; we have there K–1 independent balances: f0, f3, …, fK. In other words, f12 is not a new, independent balance in non-redox systems; it is then omitted in formulation of any non-redox system. The identity 0 = 0 for the linear combinations indicates that the equations f0, f12, f3, …, fK, are linearly dependent for non-redox systems. In a redox system, f12 is the independent balance (i.e., different from the identity, 0=0); then we have K independent balances: f0, f12, f3, …, fK, that will be rearranged – optionally – as the set (f12, f0, f3, …, fK) involved with GEB, ChB, and f(Yk) (k = 3, …, K), respectively. The number of elemental/core balances, both in non-redox and redox systems, equals K–2. Then:
• For a non-redox system, a proper linear combination of f12 with f0, f3, …, fK is reducible to identity 0 = 0, i.e., f12 is linearly dependent on f0, f3, … , fK (equations 24,25).
• For a redox system, any linear combination of f12 with f0, f3, …, fK is not reducible to identity 0 = 0, i.e., f12 is linearly independent on f0, f3, …, fK.
• In conclusion, the linear independency/dependency of f12 = 2∙f(O) – f(H) from other balances: f0, f3, …, fK is the general criterion distinguishing between redox and non-redox systems; the proper linear combination LC with dk equal to ON’s (see eq. 15), is the way towards the simplest/shortest form of GEB; the shortest form (eq. 17a) was obtained after further combination with the balance for Br (player). For a non-redox system, the linear combination indicated it is the way towards identity 0 = 0 (equations 18a, 19a).
• f12 = 2∙f(O) – f(H) is the primary form of Generalized Electron Balance (GEB), f12 = prGEB, completing the set of K balances f0, f12, f3, …, fK necessary for resolution of redox systems of any degree of complexity.
• Any linear combination of f12 with the balances f0, f3, …, fK has full properties of GEB related to the redox system considered, i.e., all them are equivalent forms of GEB.
• The Approach II to GEB does not indicate oxidants and reductants, i.e., oxidized and reduced forms in the system in question.
• The prior knowledge of oxidation numbers (ONs) for all elements of the system is not required; this fact is of capital importance when redox equilibria are involved, e.g., with complex organic species; the known composition of a species, expressed by its formula, together with external charge of this species, provides information sufficient to formulate the related balances.
• When the oxidation numbers of all elements of a system are known beforehand, the GEB can be formulated according to Approach I to GEB, known also as the 'short version' of GEB; the GEB obtained according to Approach I to GEB involves all electron-active elements – as components and species – of the system tested.
• Both Approaches (I and II) to GEB are equivalent (eq. 1).
where all ‘fans’ (K* elements or cores) of the system are involved; K* = K for a non-redox system, K* < K for a redox system, where K–K* players are involved. When dk are equal to the oxidation numbers (ONs) of elements in the corresponding ‘fans’ (k=1,…,K) of a non-redox system, then LC is transformed into identity, 0 = 0. For a redox system, LC assumes there simpler/simplest form, where only the species and components related to players are involved. The f12 is considered as the primary form of GEB, f12 = pr-GEB. The f12, LC and any other combination 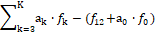 , where ak ∈ ℝ, have full properties of GEB, although the simplest/shortest form of GEB, involving the smallest number of components, is more desirable.
, where ak ∈ ℝ, have full properties of GEB, although the simplest/shortest form of GEB, involving the smallest number of components, is more desirable.
• The criterion distinguishing between non-redox and redox systems is valid for redox systems of any degree of complexity. We can check it also on more complex redox systems, of any degree of complexity, where two or more electron-active elements as ‘players’, are involved. The relation (12) was also confirmed for electrolytic systems in binary and (generally) mixed-solvent As (s = 1, …, S) media 47, 48, 49, where mixed solvates
are assumed, and niAs≥0 is the mean numbers of as molecules attached to
• The formulation of GEB according to Approach II is relatively/extraordinarily simple, although receiving the shorter equation for GEB, when using the linear combinations of pr-GEB with other balances, requires implementation of the time-consuming, preparatory activities. However, the formulation of GEB according to Approach II has – undoubtedly – the cognitive advantages, even in the cases when the oxidation numbers for all elements in the system are known beforehand.
Final Comments
The GEB concept, discovered by Michałowski as the Approaches I (1992, 2, 3, 4) and II (2005, 8) to GEB, is perceived as the law of the matter conservation, as the general Law of Nature 27, as the hidden connection of physicochemical laws, and as a breakthrough in thermodynamic theory of electrolytic redox systems. The GATES/GEB formulated in 1992, is an example of excellent paradigm, as the best possible thermodynamic approach to electrolytic redox systems. Other/earlier approaches to formulation of electrolytic redox systems, based on stoichiometric principles, were unsuccessful, for obvious reasons. All them were thoroughly criticized in our review papers 15, 16, 17, and elsewhere.
The Approach II to GEB does not require any prior knowledge of the oxidation numbers of elements in the components and in the species; it is a fact of capital importance, particularly in relation to organic species (molecules, ions, radicals and ion-radicals), of any degree of complexity. Note that the ‘oxidation number’ was essentially the contractual concept 50, 51, 52, here it results naturally from the linear combination; within the Approach II to GEB, ON is then the derivative concept. If the oxidation numbers are easily determined, the Approach I to GEB, known as the ‘short’ version of GEB, can be applied. Within the Approaches I and II to GEB, the roles/terms of oxidants and reductants are not assigned a priori to individual components; GATES/GEB provides full 'democracy' in this regard.
All the inferences made within GATES/GEB are based on firmly established physical, physicochemical and algebraic foundations. Consequently, it allows to understand far better the physicochemical phenomena occurring in the system in question, and improve some methods of analysis. All the facts testify very well about the potency of simulated calculations made, according to GATES, on the basis of all attainable and preselected physicochemical knowledge involved.
Contrary to appearances, established by the current paradigm, the criterion distinguishing non-redox and redox systems is not immediately associated with free electrons in the related system; it provides a kindof uniformity in the formulas derived for this purpose. This fact, especially the simple calculations (26,pp. 361-363) of free electrons concentrations in redox systems, deny the unique role of free electrons in elementary redox reactions, as described in half- or partial reactions, where the species of the same element with different oxidation numbers are involved. On the other hand, it points to the unique role of H and O in redox systems, suggested in earlier theoretical/hypothetical/qualitative considerations on these systems. Let’s repeat: the GEB concept, valid for redox electrolytic systems, is the emanation of balances for H and O, referred to aqueous and non-aqueous media, with amphiprotic (co)solvents involved.
Notations and Acronyms:
D – titrand (solution titrated),
GATES – Generalized Approach to Electrolytic Systems,
GEB – Generalized Electron Balance,
ON – oxidation number,
T – titrant,
V – volume (mL) of T,
V0 – volume (mL) of D.
References
- 1.Marx D, M E Tuckerman, Hutter J, Parrinello M. (1999) The nature of the hydrated excess proton in water. , Nature 397, 601-604.
- 2.Michalowski T. (1994) Calculation of pH and potential E for bromine aqueous solutions. , Journal of Chemical Education 71(7), 560-562.
- 3.Michałowski T, Lesiak A. (1994) Acid-base titration curves in disproportionating redox systems. , Journal of Chemical Education 71(8), 632-636.
- 4.Michałowski T, Lesiak A. (1994) Formulation of generalized equations for redox titration curves. , Chemia Analityczna (Warsaw) 39, 623-637.
- 5.Michałowski T, Wajda N, Janecki D. (1996) A Unified Quantitative Approach to Electrolytic Systems, Chemia Analityczna (Warsaw). 41, 667-685.
- 6.Michałowski T, Baterowicz A, Madej A, Kochana J. (2001) An extended Gran method and its applicability for simultaneous determination of Fe(II) and Fe(III), Analytica Chimica Acta. 442(2), 287-293.
- 7.Michałowski T, Toporek M, Rymanowski M. (2005) Overview on the Gran and other linearization methods applied in titrimetric analyses. , Talanta 65(5), 1241-1253.
- 8.Michałowski T, Pietrzyk A. (2006) The generalized electron balance concept. Derivation based on elementary rules of the matter conservation, in:. Chemometrics: Methods and Applications (ed. D. Zuba, A. Parczewski) , Kraków 415-422.
- 9.Michałowski T, Rymanowski M, Pietrzyk A. (2005) Non-typical Brönsted’s acids and bases. , Journal of Chemical Education 82(3), 470-472.
- 10.Michałowski T. (2007) Complementarity of physical and chemical laws of preservation in aspect of electrolytic systems (in Polish). , Wiadomości Chemiczne 61, 625-640.
- 11.Michałowski T. (2007) Complementarity of physical and chemical laws of preservation in aspect of electrolytic systems (in Polish), Use of information technology in academic teaching of chemistry. , UJ Cracow 155-161.
- 12.Michałowski T. (2007) Electron balance as the basis of calculations in redox systems (in Polish), Use of information technology in academic teaching of chemistry. , UJ Cracow 162-169.
- 13.Michałowski T, Kupiec K, Rymanowski M. (2008) Numerical analysis of the Gran methods. A comparative study. , Analytica Chimica Acta 606, 172-183.
- 14.Ponikvar M, Michałowski T, Kupiec K, Wybraniec S, Rymanowski M. (2008) Experimental verification of the modified Gran methods applicable to redox systems. , Analytica Chimica Acta 628, 181-189.
- 15.Michałowski T. (2010) The Generalized Approach to Electrolytic Systems: I. Physicochemical and Analytical Implications. , Critical Reviews in Analytical Chemistry 40, 2-16.
- 16.Michałowski T, Pietrzyk A, Ponikvar-Svet M, Rymanowski M. (2010) The Generalized Approach to Electrolytic Systems:. , II. The Generalized Equivalent Mass (GEM) Concept, Critical Reviews in Analytical Chemistry 40, 17-29.
- 17.Michałowski T. (2011) Application of GATES and MATLAB for Resolution of Equilibrium, Metastable and Non-Equilibrium Electrolytic Systems. Applications of MATLAB in Science and Engineering(ed.by T. Michałowski),InTech-Open Access publisher in the fields of Science, echnology and Medicine , Chapter 1, 1-34.
- 18.Michałowski T, Ponikvar-Svet M, Asuero A G, Kupiec K. (2012) Thermodynamic and kinetic effects involved with pH titration of As(III) with iodine in a buffered malonate system. , Journal of Solution Chemistry 41(3), 436-446.
- 19.A M Michałowska-Kaczmarczyk, Michałowski T. (2013) Comparative balancing of non-redox and redox electrolytic systems and its consequences. , American Journal of Analytical Chemistry 4, 46-53.
- 20.A M Michałowska-Kaczmarczyk, Michałowski T. (2014) GATES as the Unique Tool for Simulation of Electrolytic Redox and Non-Redox Systems. , Journal of Analytical & Bioanalytical Techniques 5(4), 1-5.
- 21.Michałowski T, Toporek M, A M Michałowska-Kaczmarczyk, A G. (2013) . New Trends in Studies on Electrolytic Redox Systems. Electrochimica Acta 109: 519-531.
- 22.Michałowski T, A M Michałowska-Kaczmarczyk, Toporek M. (2013) Formulation of general criterion distinguishing between non-redox and redox systems. , Electrochimica Acta 112, 199-211.
- 23.A M Michałowska-Kaczmarczyk, Toporek M, Michałowski T. (2015) . Speciation Diagrams in Dynamic Iodide + Dichromate System, Electrochimica Acta 155: 217-227.
- 24.Toporek M, A M Michałowska-Kaczmarczyk, Michałowski T. (2015) Symproportionation versus Disproportionation in Bromine Redox Systems. , Electrochimica Acta 171, 176-187.
- 25.A M Michałowska-Kaczmarczyk, Asuero A G, Toporek M, Michałowski T. (2015) Why not stoichiometry” versus “Stoichiometry – why not?” Part II. GATES in context with redox systems, Critical Reviews in Analytical Chemistry 45(3):. 240-268.
- 26.A M Michałowska-Kaczmarczyk, Michałowski T, Toporek M, Asuero A G. (2015) Why not stoichiometry” versus “Stoichiometry – why not?” Part III. , Extension of GATES/GEB on Complex Dynamic. Redox Systems, Critical Reviews in Analytical Chemistry 45(4), 348-366.
- 27.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Generalized Electron Balance (GEB) as the Law of Nature. in Electrolytic Redox Systems, in: Redox: Principles and Advanced Applications , Ali Khalid, M.A, (Ed.) InTech,Chap(248-pages) 2, 9-55.
- 28.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Principles of Titrimetric Analyses According to Generalized Approach to Electrolytic Systems (GATES), in:. Advances in Titration Techniques, Vu Dang Hoang (Ed.) InTech, Chap(216-pages) 5, 133-171.
- 29.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) A Distinguishing Feature of the Balance 2∙f(O) – f(H) in Electrolytic Systems. The Reference to Titrimetric Methods of Analysis, in: Advances in Titration Techniques. Vu Dang Hoang (Ed.) InTech. , Chap 6, 173-207.
- 30.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Solubility products and solubility concepts, in: Descriptive Inorganic Chemistry. , Researches of Metal Compounds. Akitsu T. (Ed.) InTech, Chap 5, 93-134.
- 31.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Formulation of simple electrolytic redox systems according to GATES/GEB principles. , Journal of Chemistry and Applied Chemical Engineering 1(1), 1-10.
- 32.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Dynamic Buffer Capacities in Redox Systems. , Journal of Chemistry and Applied Chemical Engineering 1(2), 1-7.
- 33.A M Michałowska-Kaczmarczyk, Michałowski T, Toporek M. (2016) Formulation of Dynamic Redox Systems according to GATES/GEB Principles. , International Journal of Electrochemical Science 11, 2560-2578.
- 34.Meija J, A M Michałowska-Kaczmarczyk, Michałowski T. (2017) Redox titration challenge. , Analytical and Bioanalytical Chemistry 409(1), 11-13.
- 35.Michałowski T, A M Michałowska-Kaczmarczyk, Meija J. (2017) Solution of redox titration challenge. , Analytical and Bioanalytical Chemistry 409(17), 4113-4115.
- 36.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) Some Regularities Involved with Oxidation Numbers Stated in Formulation of Redox Systems According to GATES/GEB Principles. , Journal of Analytical, Bioanalytical and Separation Techniques 2(2), 102-110.
- 37.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2018) The balance 2∙f(O) – f(H) as a keystone in formulation of electrolytic systems. Research and Reviews in Computational Chemistry 1(1), 1-9.
- 38.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) . General Properties of the Balances 2∙f(O) – f(H) Related to Electrolytic Systems, Analytical Chemistry: An Indian Journal 17(2), 124.
- 39.A M Michałowska-Kaczmarczyk, Spórna-Kucab A, Michałowski T. (2017) A general property differentiating between redox and non-redox electrolytic systems and its consequences. , International Journal of Mathematics and Statistics Invention 6(3), 67-76.
- 40.Michałowska-Kaczmarczyk A M, Michałowski T. (2018) The importance of linear algebra in theory of electrolytic systems. , Austin Chemical Engineering 5(1), print..
- 43.G H Moore. (1995) The axiomatization of linear algebra: 1875-1940. , Historia Mathematica 22(3), 262-303.
- 45.Asuero A G, Michałowski T. (2011) Comprehensive formulation of titration curves referred to complex acid-base systems and its analytical implications. , Critical Reviews in Analytical Chemistry 41(2), 151-187.
- 47.Michałowski T, Pilarski B, Asuero A G, A M Michałowska-Kaczmarczyk. (2014) . Modeling of Acid-Base Properties in Binary-Solvent Systems, Chapter9.4,pp. 623-648in “Handbook of Solvents”,Vol 1 Properties,Wypych G.(Editor),ChemTec Publishing , Toronto .
- 48.A M Michałowska-Kaczmarczyk, Michałowski T. (2014) Generalized Electron Balance for Dynamic Redox Systems in Mixed-Solvent Media. , Journal of Analytical Sciences, Methods and Instrumentation 4(4), 102-109.
- 49.A M Michałowska-Kaczmarczyk, Michałowski T. (2014) Linear Dependence of Balances for Non-Redox Electrolytic Systems. , American Journal of Analytical Chemistry 5, 1285-1289.
- 50.Karen P, McArdle P, Takats J. (2016) Comprehensive definition of oxidation state (IUPAC Recommendations. , Pure and Applied Chemistry 88(10), 831-839.
Cited by (1)
- 1.Michałowska-Kaczmarczyk Anna M., Michałowski Tadeusz, Tavakkoli Mohammad, 2020, GATES/GEB as the Best Thermodynamic Approach to Electrolytic Redox Systems - a Review, Journal of New Developments in Chemistry, 3(2), 1, 10.14302/issn.2377-2549.jndc-20-3583