Abstract
Vibrational spectral analysis and first order hyperpolarizability calculations on (E)-N′-(furan-2- ylmethylene) nicotinohydrazide (F2CNH), a novel, organic, hydrozone Schiff base compound was synthesized and its structure was characterized by FT-IR, FT-Raman and UV-visible spectrum. The optimized molecular structure, vibrational frequencies and corresponding vibrational assignments of F2CNH were performed on the basis of TED analysis using SQM method. Natural boding orbital (NBO) assessment has been carried out to clarify the charge transfer or conjugative interaction and delocalization of electron density within the molecule. Electronic transitions were studied employing UV-visible spectrum and the observed values were compared with theoretical values. The first order hyperpolarizability and related properties of F2NH were calculated. Besides FMO’s MEP, mulliken atomic charge and various thermodynamic paramefress such as Zero-point energy, rotational constant and enthalpy were also calculated and analyzed.
Author Contributions
Academic Editor: Zhe-Sheng Chenz, Professor Department of Pharmaceutical Sciences College of Pharmacy and Allied Health Professions St. John's University
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2016 Bharanidharan S, et al.
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
Furan ring as an important group of heteroaromatic compounds that have been found in many natural products and substances that have useful in industrial applications 1. It is often used as synthetic intermediates in the preparation of acyclic, carbocyclic, and heterocyclic compounds 2 and its derivatives as well as some other heterocyclic compounds are of great interest due to their application of molecules to characterise the active sites in zeolites 3, 4. Furan is a heterocyclic organic compound consisting of a five member ring with one oxygen and four carbon atoms. Furan is a colorless, flammable, highly volatile liquid with a boiling point close to room temperature. Furan is found in heat-treated commercial foods and it is produced through thermal degradation of natural food constituents 5, 6. Notably, it can be found in roasted coffee, instant coffee, and processed baby foods 7, 8. Exposure to furan at doses about 2000 times the projected level of human exposure from foods increases the risk of hepatocellular tumors in rats and mice and bile duct tumors in rats 9 and thus furan is therefore listed as a possible human carcinogen 9.
The hydrazone derivatives in the organic molecule bring several physical and chemical properties. The hydrazones are bearing the >C=N-N< which leads the molecule towards nucleophilic and electrophilic nature. The ability of hydrazones to react with both electrophilic and nucleophilic reagents widens their application in organic chemistry and designing the new drugs 10, 11, 12. Several hydrazone derivatives have been reported as insecticides, nematocides, herbicides, rodenticides and antituburculosis in addition to that some of the hydrazone were found to be active against leukemia, sarcoma and illnesses 10, 13.
Ramesh Babu et al., (2014) 14 reported the spectral Characterization of (E)-1-(Furan-2-yl) methylene)-2-(1-phenylvinyl) hydrazine (FMPVH) were carried out by using FT-IR, FT-Raman and UV–Vis spectrometry. The geometry, electronic properties, polarizability, and hyperpolarizability of 5-nitro-2-furaldehyde semicarbazone (5N2FSC) has been calculated using density functional theory (DFT) with the hybrid functional B3LYP method by Vijay Narayan et al., 2011 15. In our previous study 16, investigation on "Structural and vibrational analysis of (E)-N'-(Pyridin-2-yl) methylene nicotinohydrazide” using Quantum chemical calculation have been carried out.
According to our knowledge, neither the quantum mechanical calculations nor the vibrational spectra of the title molecule F2CNH have been reported so for. Hence the present study, we aim to interpret the vibrational spectra of F2CNH molecule by applying the ab initio/DFT computations to derive information about vibrational frequencies, IR, Raman intensities, electronic transitions and intra-molecular charge transfer, etc.
Computational Details
The entire calculations were performed at DFT levels on a Pentium 1V/3.02 GHz personal computer using Gaussian 03W 17 program package, invoking gradient geometry optimization 17, 18. In this study, the DFT/B3LYP/6-311++G(d,p)) level of basis set was used for the computation of molecular structure, vibrational frequencies and energies of optimized structures. The vibrational modes were assigned on the basis of TED analysis using VEDA4 program 19.
It should be noted that Gaussian 03W package able to calculate the Raman activity. The Raman activities were transformed into Raman intensities using Raint program 20 by the expression (1)
Where Ii is the Raman intensity, RAi is the Raman scattering activities, νi is the wavenumber of the normal modes and ν0 denotes the wavenumber of the excitation laser 21. The same formula (Eqn. 1) has been used to convert the Raman activity into Raman intensity.
Experimental Details
Synthesis Procedure
10 mL of ethanolic solution of furfural (1 mL, 0.01 mol) were added to 5 mL of aqueous solution of nicotinic acid hydrazide (1.37 g, 0.01 mol) and stirred well for an hour in the presence of hydrochloric acid to form a white precipitate. The reaction mixture was maintained at room temperature and the colourless solid was obtained. The solid was separated and filtered under suction, washed with ice-cold water. The precipitate was washed with water and filtered and again washed with petroleum ether (40-60%) and dried over in a vacuum desicator then the product was recrystallized from hot ethanol.
Results and Discussion
Molecular Geometry
The optimized bond parameters of F2CNH was carried out using DFT/B3LYP/6-311++G(d,p) basis set and are listed in Table 1. The optimized structure is shown in Figure 1. The title molecule consist of pyridin and furan ring linked by hydrazone linkage. The hydrazone linkage plays an important role in F2CNH. The electronic coupling between the amino hydrogen (N12-H13), carbonyl (C14=O15) lone pairs electrons and the (C14-C16) pyridine ring π-system creates phenyl N, O conjugations. This conjugations bring about intra-molecular charge (ICT) transfer. In the ICT state, the nπ interactions are substantially decreased, and thereby an electronic decoupling occurs from the ring π-system 22, which causes the differences in bond lengths of C9=N11 (1.282Å), C14-N12 (1.385Å) and also the variation of bond angles of C14-C16-C17 (117.59°) and C14-C16-C18 (123.59°). The bond distance of C14-N12 is well below the single bond distance which indicates the electron delocalization over the region of the molecule and it is supported by literature 22.
Table 1. The optimized bond parameters of F2CNH| Parametres | B3LYP/6-311++G( d,p ) | XRD * |
| Bond Lengths (Å) | ||
| O1-C2 | 1.372 | 1.366 |
| O1-C5 | 1.358 | 1.368 |
| C2-C3 | 1.369 | 1.348 |
| C2-C9 | 1.441 | 1.432 |
| C3-C4 | 1.425 | 1.415 |
| C3-H6 | 1.077 | 0.930 |
| C4-C5 | 1.362 | 1.368 |
| C4-H7 | 1.078 | 0.930 |
| C5-H8 | 1.076 | 0.930 |
| C9-N11 | 1.282 | 1.273 |
| N11-N12 | 1.356 | 1.384 |
| N12-H13 | 1.015 | 0.860 |
| N12-C14 | 1.385 | 1.348 |
| C14-O15 | 1.212 | 1.230 |
| C14-C16 | 1.502 | 1.490 |
| C16-C17 | 1.398 | 1.387 |
| C16-C18 | 1.399 | 1.379 |
| C17-C19 | 1.387 | 1.380 |
| C17-H20 | 1.083 | 0.93 |
| Bond Angles (°) | ||
| O1-C2-C3 | 109.67 | 110.11 |
| O1-C2-C9 | 115.72 | 119.36 |
| C3-C2-C9 | 134.59 | 130.51 |
| C2-C3-C4 | 106.38 | 106.54 |
| C2-C3-H6 | 125.49 | 126.70 |
| C4-C3-H6 | 128.11 | 126.7 |
| C3-C4-C5 | 106.40 | 106.65 |
| C3-C4-H7 | 127.33 | 126.70 |
| C5-C4-H7 | 126.25 | 126.7 |
| O1-C5-C4 | 110.45 | 111.01 |
| O1-C5-H8 | 115.96 | 124.5 |
| C4-C5-H8 | 133.58 | 124.5 |
| C2-C9-H10 | 116.03 | 119.10 |
| C2-C9-N11 | 121.14 | 121.81 |
| H10-C9-N11 | 122.81 | 119.10 |
| C9-N11-N12 | 116.86 | 116.43 |
| N11-N12-H13 | 119.33 | 120.40 |
| N11-N12-C14 | 121.07 | 119.16 |
| H13-N12-C14 | 119.31 | 120.4 |
| N12-C14-O15 | 123.61 | 122.65 |
| Bond Angles (°) | ||
| N12-C14-C16 | 114.22 | 116.08 |
| O15-C14-C16 | 122.15 | 121.24 |
| C14-C16-C17 | 117.98 | 117.59 |
| C14-C16-C18 | 124.29 | 123.59 |
| C16-C17-C19 | 118.94 | 118.82 |
| C16-C17-H20 | 119.08 | 119.9 |
| C19-C17-H20 | 121.96 | 119.9 |
| C16-C18-H22 | 120.92 | 120.39 |
| C23-C19-H24 | 120.27 | 120.01 |
| C19-C23-H25 | 120.52 | 120.0 |
| Dihedral Angles (°) | ||
| O1-C2-C9-N11 | 179.75 | |
| C3-C2-C9-H10 | 179.90 | |
| C3-C2-C9-N11 | -0.20 | |
| C2-C3-C4-C5 | 0.00 | |
| C2-C3-C4-H7 | 179.99 | |
| H6-C3-C4-C5 | -179.98 | |
| H6-C3-C4-H7 | 0.01 | |
| C3-C4-C5-O1 | -0.01 | |
| C3-C4-C5-H8 | 179.99 | |
| H7-C4-C5-O1 | -180.00 | |
| H7-C4-C5-H8 | -0.00 | |
| C2-C9-N11-N12 | -179.48 | |
| H10-C9-N11-N12 | 0.40 | |
| C9-N11-N12-H13 | -1.96 | |
| C9-N11-N12-C14 | -175.84 | |
| N11-N12-C14-O15 | 2.95 | |
| N11-N12-C14-C16 | -177.75 | |
| H13-N12-C14-O15 | -170.92 | |
| H13-N12-C14-C16 | 8.37 | |
| N12-C14-C16-C17 | -154.58 | |
| N12-C14-C16-C18 | 28.13 | |
| O15-C14-C16-C17 | 24.72 |
Figure 1.The optimized structure of (E)-N′-(furan-2-ylmethylene)nicotinohydrazide (F2CNH)
The bond angle of O15=C14-C16 is calculated at 121.24°, which is in agreement with literature value 122.15 and also finds support from literature Song and Fan, (2009) 23. In hydrazone linkage, the angle for C9=N11-N12 was calculated about 116.86° whereas the literature value is 116.43° 22. The bond angles of C16-C17-H20 (119.09°) is negatively ~2.8° deviated from C19-C17-H20 (121.96°), which is due to the presence of O15 atom next to H20 atom. The furan ring moiety is planar [C3-C2-C9-N11 = -0.20° and O1-C2-C9-N11 = 179.75°] with hydrazone linkage, while phenyl ring is not planar [C17-C16-C14-N12 = -154.58° and C18-C16-C14-N12 = 28.13°]. Most of the calculated bond parameters are comparable with XRD values and also find support from the literature values of related structure [24, 25].
Vibrational Analysis
The fundamental vibrations of a non-linear molecule which contains N atoms is equal to (3N-6), apart from three translational and three rotational degrees of freedom 26, 27. The F2CNH molecule belongs to Cs point group symmetry and has 25 atoms; hence 69 normal modes of vibrations are possible. The fundamental modes are distributed as: Гvib = 47A′ + 22A′′. All vibrations are active in both IR and Raman absorption. The harmonic wavenumbers were calculated using DFT/B3LYP/6-311++G(d,p) basis set and are listed in Table 2. The vibrational assignments were made by visual inspection of modes animated by using the Gauss view 17 program and are also justified with the help of TED analysis. The combined vibrational spectra of F2CNH are shown in Figure 2 and Figure 3.
Figure 2.The Theoretical and Experimental FT-IR spectra of F2CNH
Figure 3.The Theoretical and Experimental FT-Raman spectra of F2CNH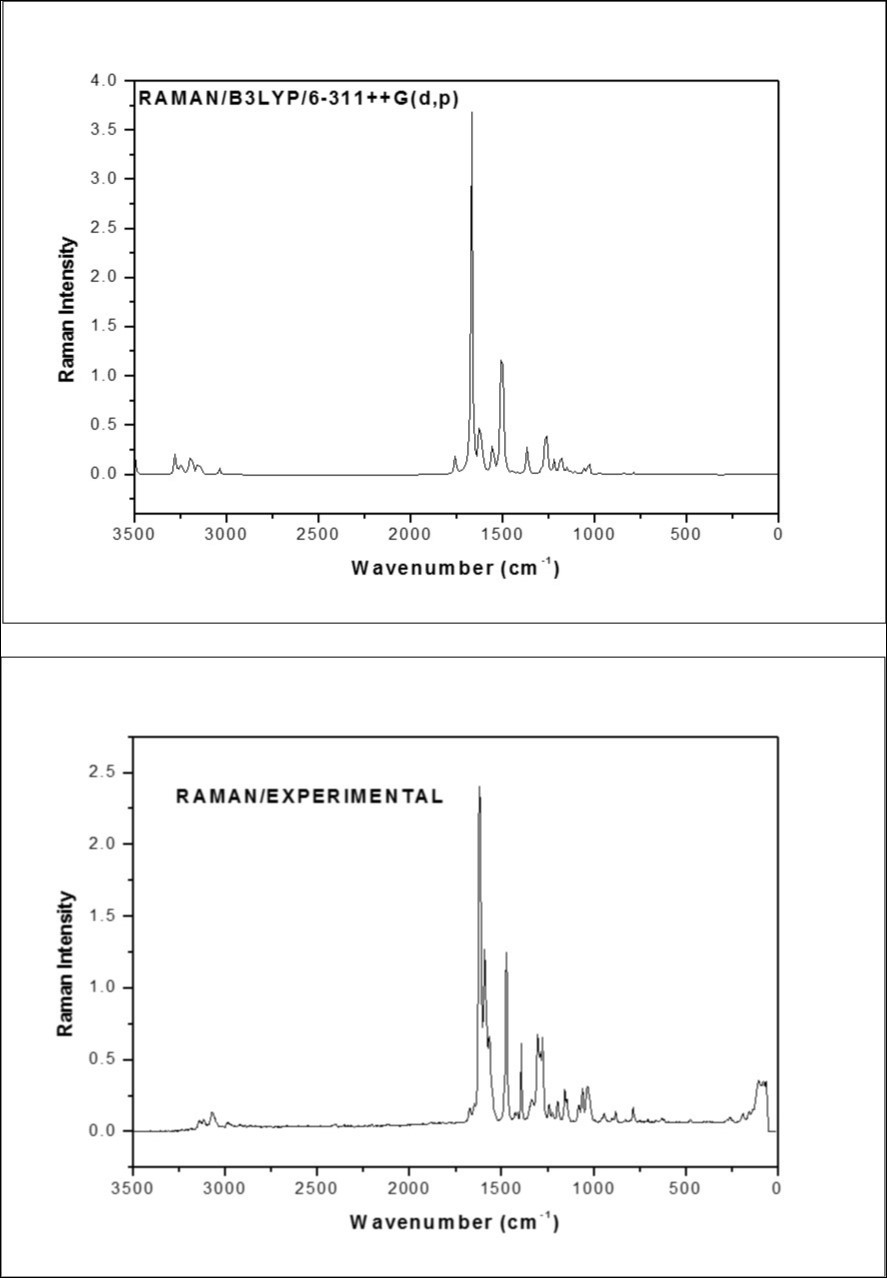
C-H Vibrations
The heteroaromatic molecule shows the presence of C-H stretching mode in the region 3100-3000 cm-1 which is the characteristic region for the ready identification of C-H stretching 28, 29. In this molecule, nine C-H stretching vibrations are expected to occur in which, four from pyridin ring, three from furan ring and one from hydrazone linkage. The pyridin ring C-H stretching vibrations observed at 3069 (m) in FT-IR whereas FT-Raman shown at 3071 and 2986cm-1 which is moderately in line with our earlier study 16. The calculated wavenumbers for the same mode lies at 3076, 3061, 3032 and 3016 cm-1 (mode nos: 5-8). The experimental C-H stretching modes corresponding to furan ring are assigned to 3120 cm-1/FT-IR and 3117 cm-1 in FT-Raman and their harmonic value lies at 3151, 3135 and 3119 cm-1 (mode nos: 2-4). The C-H stretching in hydrazone linkage is calculated at 2919 cm-1 and its corresponding experimental value at 2926 cm-1 in FTIR spectrum (mode no: 9) which is close to the value of literature 16. Furthermore, these assignments are in good agreement with literature 28, 29, 30 and also find support from TED value ≥ 85%.
In aromatic compounds the C-H in-plane bending mode appear in the range 1300–1000 cm-1 and C-H out-of-plane bending mode appear in the range 1000-750 cm-131, 32. In the pyridine moiety of F2CNH, we observed the βCH modes at 1469, 1295 cm-1 (FT-IR)/ 1304, 1081 cm-1 (FT-Raman) and ΓCH modes at 825 (FT-Raman)/827, 705 cm-1 (FT-IR) and their corresponding calculated frequencies are in the range of 1449-1090 cm-1 (mode nos: 16, 21, 25, 29) and 948-710 cm-1 (mode nos: 36, 39, 43, 47), respectively. On comparing these observed values with calculated values, the mode numbers 21, 29 and 36, 43 are having ≥42% of TED value.
The bands between 1230 and 970 cm-1 in furan are assigned to βCH modes 33. The bands for the in-plane/ out-of-plane bending modes of CH in furan ring are identified at 1153/787 cm-1 in FTIR/FT-Raman spectra. For the same mode the corresponding harmonic frequencies are: 1219, 1138, 993 cm-1 (mode nos: 23, 27, 34) and 859, 802, 720 cm-1 (mode nos: 42, 44, 46), respectively. These assignments are in good agreement with the assignments proposed by Subramanian et al., (2010) 34 and Balachandran et al., (2013) 33. Further, the mode nos: 20 and 38 are attributed respectively to βCH and ΓCH modes of hydrazone linkage. These assignments are made in accordance with the assignments proposed by Ramesh Babu et al., (2014) 14 and also find support from observed FTIR band 1337 cm-1. All the deformations (βCH and ΓCH) are having considerable TED values.
C=O, C-O Vibrations
The C=O stretching band is characterized by a sharp intense band appearing in between 1680 and 1715 cm-135, 36. According to this, the sharp intense bands in FTIR: 1682/FT-Raman: 1673 cm-1 spectra are assigned to C14=O15 stretching mode, were as in our previous study 16 values shown at 1661/1663 in FT-IR/FT Raman respectively which is also confirmed by literature 14 and also find support from harmonic value: 1689 cm-1 (mode no: 10). The βC14=O15 mode is assigned at 881 cm-1 (mode no: 40) in comparison with literature 14. In our study, the bands observed at 878 and 882 cm-1 are due to βC=O mode in FTIR and FT-Raman spectra, respectively. The calculated TED (40%) corresponding to this mode shows that this mode is not a pure mode but contaminated with βCNN and βCOC modes as shown in Table 2. The mode no: 47 (710 cm-1) having TED value (45%) is attributed to ΓC=O mode, which is in agreement with the observed FTIR bands at 705 cm-1. These C=O deformations vibrations are well supported by literature 14.
Table 2. The experimental and calculated frequencies of F2CNH using B3LYP/ 6-311++G(d,p) level of basis set harmonic frequencies (cm−1) IR Raman intensities (Km/mol) reduced masses (amu) and force constants (mdynA°−1)| Mode No | Calculated Frequencies (cm -1 ) | Observed Frequencies (cm -1 ) | IR Intensity | Raman Intensity | Vibrational Assignments≥10% (TED) d | |||
| Scaled a | FT-IR | FT-Raman | Rel. b | Rel. c | ||||
| 1 | 3367 | 2.01 | 1.55 | ѴN12H13(100) | ||||
| 2 | 3151 | 0.07 | 1.09 | ѴC5H8(84) | ||||
| 3 | 3135 | 0.24 | 0.22 | ѴC3H6(86) | ||||
| 4 | 3119 | 3120 w | 3117 w | 1.07 | 0.74 | ѴC4H7(85) | ||
| 5 | 3076 | 3071 w | 1.90 | 0.89 | ѴC17H20(90) | |||
| 6 | 3061 | 3069 m | 2.58 | 1.04 | ѴC19H24(94) | |||
| 7 | 3032 | 3.04 | 0.88 | ѴC23H25(92) | ||||
| 8 | 3016 | 2986 w | 8.10 | 0.37 | ѴC18H22(98) | |||
| 9 | 2919 | 2926 w | 10.18 | 0.45 | ѴC9H10(100) | |||
| 10 | 1689 | 1682 m | 1673 w | 100.00 | 5.15 | ѴO15C14(85) | ||
| 11 | 1604 | 1633 s | 1621 s | 6.67 | 100.00 | ѴN11C9(73)+βH10C9N11(11) | ||
| 12 | 1563 | 1561 m | 1568 m | 8.77 | 14.37 | ѴC17C19(26)+βC17C16C18(11) | ||
| 13 | 1553 | 17.15 | 8.42 | ѴC4C5(15)+ѴC2C3(42)+ѴC9C2(14) | ||||
| 14 | 1542 | 1.53 | 0.51 | ѴN21C23(20)+ѴC23C19(24)+βC16C18N21(16)+βC18N21C23(13) | ||||
| 15 | 1495 | 1475 s | 99.44 | 12.34 | ѴN12C14(12)+βH13N12N11(58) | |||
| 16 | 1449 | 1469 m | 6.60 | 31.71 | ѴC4C5(22)+βH24C19C17(15)+βH22C18C16(15) | |||
| 17 | 1443 | 1428 m | 1426 w | 2.74 | 31.53 | ѴC4C5(43)+βH8C5O1(31) | ||
| 18 | 1391 | 1394 m | 7.33 | 0.73 | βC16C18N21(22)+βH25C23N21(42) | |||
| 19 | 1367 | 3.46 | 0.64 | ѴC4C3(22)+βH7C4C5(18)+βH8C5O1(13)+βH10C9N11(10) | ||||
| 20 | 1315 | 1337 s | 12.87 | 10.80 | ѴC4C3(24)+βH10C9N11(40) | |||
| 21 | 1308 | 1295 w | 1304 m | 1.38 | 0.86 | βH20C17C19(29)+βH22C18C16(39) | ||
| 22 | 1240 | 1244 w | 5.38 | 1.75 | ѴC17C19(18)+ѴN21C18(48) | |||
| 23 | 1219 | 35.93 | 5.09 | ѴC4C3(11)+βH6C3C4(24)+βH8C5O1(13) | ||||
| 24 | 1215 | 1214 m | 1198 w | 46.30 | 25.24 | βC17C16C18(11)+ѴC16C14(17)+βH6C3C4(10) | ||
| 25 | 1174 | 13.24 | 6.89 | ѴN21C23(27)+βH24C19C17(11)+βH25C23N21(20) | ||||
| 26 | 1170 | 1158 w | 0.80 | 0.63 | ѴO1C2(31)+βH10C9N11(15) | |||
| 27 | 1138 | 1153 m | 21.11 | 14.35 | ѴO1C5(19)+ѴN12N11(21)+βH8C5O1(20) | |||
| x | 1108 | 45.00 | 4.24 | ѴN12C14(12)+ѴN12N11(15)+βH8C5O1(15) | ||||
| 30 | 1067 | 1062 m | 1062 w | 13.11 | 1.64 | ѴC4C5(12)+ѴO1C5(43) | ||
| 31 | 1041 | 1035 w | 4.01 | 0.58 | ѴN12C14(14)+ѴN12N11(23) | |||
| 32 | 1016 | 1020 m | 0.37 | 3.90 | ѴN21C23(16)+ѴC23C19(36) | |||
| 33 | 999 | 4.05 | 2.29 | βC18N21C23(24)+βC19C23N21(18)+βC23C19C17(36) | ||||
| 34 | 993 | 6.44 | 7.61 | ѴC4C3(28)+βH6C3C4(30)+βH7C4C5(29) | ||||
| 35 | 974 | 0.67 | 0.07 | τH20C17C19H24(77)+τH25C23N21C18(16) | ||||
| 36 | 948 | 945 w | 0.31 | 0.06 | ГC17C16C19H20(31)+ГC18C16C21H22(11)+τH25C23N21C18(47) | |||
| 37 | 938 | 938 w | 5.90 | 1.77 | ѴC2C3(13)+ѴO1C2(27)+βC2O1C5(20) | |||
| 38 | 910 | 3.58 | 0.52 | τH10C9N11N12(86) | ||||
| 39 | 909 | 0.39 | 0.09 | ГC18C16N21H22(72) | ||||
| 40 | 881 | 878 w | 882 w | 4.65 | 0.32 | βN12C14O15(40)+βC14N12N11(11)+βC2O1C5(17) | ||
| 41 | 867 | 5.71 | 0.63 | βC4C3C2(45)+βC2O1C5(34) | ||||
| 42 | 859 | 0.05 | 0.23 | τH6C3C4C5(31)+τH7C4C5H8(53)+τH8C5C4C3(10) | ||||
| 43 | 807 | 827 w | 2.42 | 1.33 | ГC17C16C19H20(34)+τH20C17C19H20(16)+ГO15C16N12C14(13)+ГC18C16N21H22(20) | |||
| 44 | 802 | 787 w | 4.00 | 0.04 | τH6C3C4C5(55)+τH7C4C5H8(34) | |||
| 45 | 759 | 756 m | 6.99 | 1.88 | βN11C9C2(18)+βC4C3C2(15)+βC2O1C5(19)+ГC14C16C18C17(20) | |||
| 46 | 720 | 19.50 | 0.41 | τH7C4C5H8(12)+τH8C5C4C3(75) | ||||
| 47 | 710 | 705 w | 6.96 | 0.70 | ГC17C16C19H20(15)+ГO15C16N12C14(45) | |||
| 48 | 696 | 5.95 | 0.36 | βC19C23N21(19)+τC16C23C18N21(15)+τC19C17C23N21(11) | ||||
| 49 | 690 | 5.30 | 0.09 | τC16C23C18N21(27)+τC18N21C19C23(16)+τC19C17C23N21(21) | ||||
| 50 | 640 | 0.02 | 0.08 | τC3C2C4C5(12)+τC3C5C2O1(66) | ||||
| 51 | 609 | 1.10 | 0.60 | βC16C18N21(20)+βC18N21C23(32)+βC23C19C17(28) | ||||
| 52 | 581 | 582 w | 2.36 | 0.10 | τC3C2C4C5(50)+τC3C5C2O1(26) | |||
| 53 | 523 | 521 w | 2.31 | 1.21 | βC16C18N21(24)+ГH13N12N11C9(30) | |||
| 54 | 493 | 13.68 | 1.56 | τH13N12N11C9(80) | ||||
| 55 | 466 | 0.35 | 1.05 | βC17C16C18(12)+βN11C9C2(11)+βC9C2O1(18) | ||||
| 56 | 405 | 419 w | 2.43 | 0.12 | τC16C23C18N21(19)+τC18N21C19C23(32) | |||
| 57 | 383 | 0.83 | 0.13 | τC16C23C18N21(16)+τC19C17C23N21(32) | ||||
| 58 | 370 | 0.37 | 0.09 | βC17C16C18(15)+ѴC16C14(14)+βN12C14O15(19)+τN12N11C9C2(11) | ||||
| 59 | 348 | 0.42 | 0.43 | τN12N11C9C2(29)+τC5O1C2C9(14) | ||||
| 60 | 258 | 3.81 | 0.42 | βC18C16C14(32) | ||||
| 61 | 238 | 0.14 | 1.01 | βC9C2O1(20)+βC14N12N11(21) | ||||
| 63 | 167 | 191 w | 3.13 | 1.44 | βC18C16C14(10)+τC3C2C9N11(18)+τC14N12N11C9(24)+ГC14C16C18C17(14) | |||
| 64 | 131 | 0.76 | 1.19 | τC14N12N11C9(15)+τN12N11C9C2(11)+τC5O1C2C9(41) | ||||
| 65 | 118 | 107 w | 2.15 | 0.78 | βN11C9C2(19)+βC9C2O1(14)+βC16C14N12 (18)+ГC14C16C18C17(13) | |||
| 66 | 66 | 1.44 | 3.86 | τC3C2C9N11(16)+τC18C16C14N12(41)+τC14N12N11C9(13)+τC5O1C2C9(11) | ||||
| 67 | 47 | 0.23 | 2.59 | βN11C9C2(16)+βC14N12N11(23)+βN12N11C9(19)+βC16C14N12(15) | ||||
| 68 | 35 | 0.05 | 4.48 | τC3C2C9N11(24)+τN12N11C9C2(23)+τC16C14N12N11(36) | ||||
| 69 | 31 | 0.73 | 8.59 | τC18C16C14N12(41)+τC14N12N11C9(26)+τC16C14N12N11(14) | ||||
According to Ramesh Babu et al., (2014) 14, the harmonic frequencies of C-O stretching in furan ring appear in the range 1193-905 cm-1. The frequency of the νO1-C5 and νO1-C2 vibrations are calculated to be 1170 and 1067 cm-1, respectively for F2CNH and these modes are observed in the FT-Raman spectrum at 1158 and 1062 cm-1 (FTIR: 1062 cm-1) with weak intensity. These assignments are well within the expected range and they have considerable TED values (31% and 43%). The βCOC (mode nos: 37, 45) and τCOC (mode nos: 59, 64) vibrations are presented in Table 2. These assignments are also supported by the literature 33 in addition to TED output.
C=N, C-N and N-N Vibrations
The IR and Raman bands observed between 1443 and 1227 cm-1 in pyridine derivatives have been assigned to νC-N vibrations 37. In general, a pure mode cannot be expected for νC-N vibrations since it falls in a complicated region of the vibrational spectrum. In F2CNH the C18-N21/C23-N21 stretching vibrations assigned at 1240/1542 cm-1 (mode nos: 22, 14) as mixed vibrations of νCC+βCCN/βCCC+βHCN modes respectively. In which mode no: 22 correlates well with observed FT-Raman value 1244 cm-1 and also find support from TED value 48%.
In this work, the hydrazone linkage fuses the pyridine and furan rings, which leads the vibrations such as νC=N, νC-N and νN-N modes. According to Socrates (1980) 31 the frequencies of νC=N appear around 1600-1670 cm-1. In our earlier study, the νC=N vibration assigned at 1611: FTIR/1627 cm-1: FT-Raman 14. In our earlier investigation 16, FT-Raman shown at 1606 and Rameshbabu et, al., 14 assigned νC=N, vibration at 1611:FTIT / 1627:FT-Raman. Based on these literature, the scaled harmonic wavenumber of νC9=N11 mode depicted in Table 2 (1604 cm-1/mode no: 11) is found to be in agreement with experimental data: 1633 cm-1 in FTIR as well as in FT-Raman spectra (1621 cm-1). Silverstein et al., (1981) 29 assigned C-N stretching absorption in the region 1382-1266 cm-1 for aromatic amines. In the present study, the band observed at 1475 cm-1 in FT-Raman spectrum which is exactly matches with our earlier study 14 at 1606/FT-Raman and its corresponding calculated value 1495 cm-1 (mode no: 15) are assigned to νC14-N12 mode. The same mode was recorded at 1516 cm-1 (FTIR) by Rameshbabu et. Al., 14. The νN-N mode was observed as a medium intense band at 1128 cm-1 /FTIR and at 1137 cm-1/FT-Raman 22. The νN11-N12 vibration is observed as a medium intense band in FTIR at 1153 cm-1 (Harmonic/mode no: 27/1138 cm-1) has 21% of this stretching character because of its association with νCO and βHCO vibrations and this assignment is further supported by literature 14.
The βC2-C9=N11/ΓC2-C9=N11 vibrations are assigned at 756 (FTIR)/348 cm-1 (harmonic) and that of βC14-N12-N11/ΓC14-C12-N11 are assigned at 878 (FTIR)/191 cm-1 (FTIR) respectively, in comparison with their corresponding harmonic values (mode nos: 45/59 and 40/63). The theoretically computed values for βC9=N11-N12 and ΓC9=N11-N12 vibrations come out to be 47 cm-1 (mode no: 67) and 31 cm-1 (mode no: 69) respectively. These assignments are having considerable TED values.
N-H Vibrations
The N-H stretching vibrations occur in the region 3400-3200 cm-138 and Ramesh babu et. al., 14 observed at 3246 cm-1 in FTIR spectrum. In agreement with these observation, in the present case also this band at 3367 cm-1 (mode no: 1) is assigned to stretching frequency of N-H group. This assignment is straight forward on the basis of their calculated TED value (100 %). The calculated wavenumber for βN-H (1495 cm-1/mode no: 15) and ΓN-H (523 cm-1/ mode no: 53) modes well reproduced the experimental ones in FT-Raman (1475 cm-1) and FTIR (521 cm-1) spectra, respectively. These assignments are made in accordance with the literature 14 and also find support from their respective TED values (58% and 30%).
C=C, C-C Vibrations
In furan derivatives, medium to strong bands have appeared in the regions of 1390-1400, 1470-1520, 1560-1610 cm-1, which are due to the C=C ring stretching vibrations 27. In general, furan with electronegative substituent has strong bands in these regions. Usually Five membered ring compounds with two doublet bond in ring, shows three ring stretching bands near 1400, 1490 and 1590 cm-139.
In our present study, the C=C stretching bands observed at 1469 (m), 1428 (m), and 1337 cm-1 (s) in FT-IR spectrum, whereas FT-Raman band observed at 1426 as weak band. On the other hand, νc=c bands were predicted at 1449, 1443 and 1315 cm-1 (mode nos: 16, 17 and 20) and in good agreement with literature 14. The mode nos: 41, 45 and 50, 52 are belong to βCCC and ΓCCC modes, respectively. In which mode nos: 45 (759 cm-1) and 52 (581 cm-1) are justified by the observed FTIR bands at 756 and 582 cm-1 and also find support from TED value.
The C-C stretching was assigned in the region 1668-1218 cm-1 for some substituted pyridines 37. Ramesh Babu et al., 40 assigned 1532 (w), 1370, 1261 cm-1 in FT-Raman and 1361, 1266 cm-1 (w) in FTIR spectra are assigned to ν(C-C) vibrations of pyridine ring in the case of (E)-N′-((pyridine-2-yl)methylene)benzohydrazide. In view of the above, the harmonic frequencies in the range 1563-1016 cm-1 (mode nos: 12, 22, 29, 32) and the bands observed at 1561, 1020/1568, 1244, 1081 cm-1 in FTIR/FT-Raman spectra are assigned to νC-C mode. These assignments are also supported by TED value.
The βCCC and ΓCCC modes associated with smaller force constant than the stretching one and hence assigned to lower frequencies. The harmonic frequencies 999, 609 and 405, 383 cm-1 (mode nos: 33, 51 and 56, 57) are assigned to βCCC and ΓCCC modes of pyridine ring. These assignments find support from literature 40 in addition to TED output. Further, the mode no: 56 is further supported by observed band (FTIR/419 cm-1). The mode nos: 13 and 24 are belong to νC9-C2 and νC16-C14 modes.
NLO Property
The molecular electronic dipole moment and molecular first hyperpolarizability of F2CNH were calculated using B3LYP level and the obtained results were given in Table 3. The dipole moment was calculated as 0.9722 Debye which is comparatively closer to standard urea. The first order hyperpolarizability (β0)was calculated as 2.0918x10-30 esu, which is six times greater than that of the value of the urea. Hence this molecule has considerable NLO activity.
Table 3. The NLO measurements of F2CNH| Parameters | B3LYP/6-311++G(d,p) |
| Dipole moment ( μ ) Debye | |
|---|---|
| μx | -0.3453 |
| μy | -0.7229 |
| μz | 0.5508 |
| μ | 0.9722Debye |
| Polarizability ( α0 ) x10-30esu | |
| αxx | 313.9112 |
| αxy | 0.06 |
| αyy | -0.0037 |
| αxz | 0.0048 |
| αyz | -0.0112 |
| αzz | 0.1032 |
| αo | 0.6277x10-30esu |
| Hyperpolarizability ( β0 )x10-30esu | |
| βxxx | 2472.1702 |
| βxxy | 254.6161 |
| βxyy | 15.47 |
| βyyy | -93.8977 |
| βxxz | 30.3521 |
| βxyz | -22.69 |
| βyyz | 12.4543 |
| βxzz | -72.4323 |
| βyzz | -0.8853 |
| βzzz | 19.7437 |
| β0 | 2.0918x10-30esu |
NBO Analysis
The NBO analysis has been carried out with B3LYP/6-311++G(d,p) level of basis set. The Lewis and non-Lewis NBO’s of the F2CNH are given in Table 4. The strong intra-molecular hyper conjucative interaction of the π and σ electrons of C-C to the anti C-C bond of the rings lead to stabilization of some part of the rings. The intra-molecular hyper cnjucative interaction of π(C2-C3)→π*(C9-N11), π(C9-N11)→π*(C2-C3) and π(N21-C23)→π*(C16-C18) leading to stabilization of 75.48, 41.17 and 113.09 KJ/mol, respectively. On the other hand the σ(C2-C3)→σ*(C2-C9), σ(C9-N11)→σ*(N12-C14) and σ(C17-C19)→σ*(C16-C17) transition stabilize lesser energy 17.87, 9.46 and 12.01 KJ/mol, respectively. In such a way that the molecule F2CNH delivers maximum delocalization energy during π-π* transition whereas the electron density of the donor (Lewis) bond decreases with increasing of electron density of acceptor (Non-Lewis) bonds. The maximum energy transfer during the intra-molecular interaction between (π-π*) (C17-C19) and (N21-C23) is about 122.13 KJ/mol. This may be due to the hyperconjucative interaction between C17-C19 donor and C23-N21 acceptor bonds. It is evident from Table 4, the π(C17-C19) hyperconjucative interactions transfer more energy (122.13 KJ/mol) to the acceptor bond π*(N21-C23) in pyridine ring. Hence the strong delocalization in pyridine is mainly due to the presence of C=N-C. Based on the fact, that the ν(C23-N21) modes appear at higher frequency (1542 cm-1) on comparing with ν(C18-N21/1240 cm-1 mode. In F2CNH, the π-π* interaction appear with maximum delocalization energy which leads the molecule become highly active. The lone pair of oxygen and nitrogen atoms play greater role in the molecule F2CNH: LPO1→C4-C5 (114.47), LPO15→N12-C14 (118.41) and LPN12→C14-O15 (190.62 KJ/mol), respectively. These charge transfer interactions of F2CNH are responsible for more stabilization, medicinal and biological properties.
Table 4. The second order perturbation theory analysis of Fock Matrix in NBO basis for F2CNH| Type | Donor NBO (i) | ED/e | Acceptor NBO (j) | ED/e | E(2) KJ/mol | E(j)-E(i) a.u. | F(i,j) a.u. |
| σ -σ* | BD (1) C2 - C3 | 1.98 | BD*(1) C2 - C9 | 0.028 | 17.87 | 1.21 | 0.06 |
| BD*(1) C3 - C4 | 0.009 | 7.61 | 1.25 | 0.04 | |||
| BD*(1) C3 - H6 | 0.011 | 5.44 | 1.18 | 0.04 | |||
| BD*(1) C4 - H7 | 0.011 | 15.56 | 1.17 | 0.06 | |||
| BD*(1) C9 - H10 | 0.035 | 4.85 | 1.09 | 0.03 | |||
| π -π* | BD (2) C2 - C3 | 1.792 | BD*(2) C4 - C5 | 0.268 | 70.42 | 0.29 | 0.06 |
| BD*(2) C9 - N11 | 0.214 | 75.48 | 0.27 | 0.06 | |||
| σ -σ* | BD (1) C9 - N11 | 1.986 | BD*(1) N12 - C14 | 0.085 | 9.46 | 1.33 | 0.05 |
| BD*(1) C2 - C9 | 0.028 | 7.82 | 1.39 | 0.05 | |||
| π -π* | BD (2) C9 - N11 | 1.925 | BD*(2) C2 - C3 | 0.315 | 41.17 | 0.37 | 0.06 |
| σ -σ* | BD (1) C17 - C19 | 1.979 | BD*(1) C16 - C17 | 0.021 | 12.01 | 1.27 | 0.05 |
| π -π* | BD (2) C17 - C19 | 1.636 | BD*(2) C16 - C18 | 0.336 | 74.81 | 0.28 | 0.06 |
| BD*(2) N21 - C23 | 0.366 | 122.13 | 0.27 | 0.08 | |||
| π -π* | BD (2) N21 - C23 | 1.706 | BD*(2) C16 - C18 | 0.336 | 113.09 | 0.32 | 0.08 |
| BD*(2) C17 - C19 | 0.277 | 52.59 | 0.32 | 0.06 | |||
| n -π* | LP (2) O1 | 1.708 | BD*(2) C2 - C3 | 0.315 | 108.78 | 0.37 | 0.09 |
| BD*(2) C4 - C5 | 0.268 | 114.47 | 0.36 | 0.09 | |||
| n -π* | LP (2) N12 | 1.666 | BD*(2) C9 - N11 | 0.214 | 117.24 | 0.28 | 0.08 |
| BD*(2) C14 - O15 | 0.277 | 190.62 | 0.32 | 0.11 | |||
| n -π* | LP (2) O15 | 1.855 | BD*(2) N12 - C14 | 0.085 | 118.41 | 0.67 | 0.12 |
| BD*(2) C14 - C16 | 0.069 | 80.33 | 0.66 | 0.1 | |||
| n -σ* | LP (1) N21 | 1.916 | BD*(1) C16 - C18 | 0.033 | 39.33 | 0.9 | 0.08 |
| BD*(1) C18 - H22 | 0.025 | 17.32 | 0.76 | 0.05 | |||
| BD*(1) C19 - C23 | 0.026 | 37.45 | 0.9 | 0.08 | |||
| BD*(1) C23 - H25 | 0.023 | 16.99 | 0.77 | 0.05 | |||
| π*-π* | BD*(2) C9 - N11 | 0.214 | BD*(2) C2 - C3 | 0.315 | 330.75 | 0.02 | 0.08 |
| π*-σ* | BD*(2) C14 - O15 | 0.277 | BD*(1) C14 - O15 | 0.017 | 12.59 | 0.56 | 0.1 |
| π*-π* | BD*(2) C16 - C18 | 0.336 | BD*(2) C14 - O15 | 0.277 | 369.99 | 0.02 | 0.07 |
| π*-π* | BD*(2) N21 - C23 | 0.366 | BD*(2) C16 - C18 | 0.336 | 839.56 | 0.01 | 0.08 |
| BD*(2) C17 - C19 | 0.277 | 590.7 | 0.02 | 0.08 |
HOMO-LUMO Analysis
The HOMO and LUMO are the main orbital’s that take part in chemical stability. The HOMO represents the ability to donate an electron, whereas the LUMO is an electron acceptor which represents the ability to obtain an electron. This also predicted that the nature of electrophiles and nucleophiles to an atom where the HOMO and LUMO are stronger. The energy gap of F2CNH was calculated using B3LYP/6-311++G(d,p) level and are listed in Table 5. In the present study, the HOMO part is located over the furan ring and hydrazone linkage and HOMO energy is calculated about -6.032 eV. Similarly, the LUMO is located over the entire molecule and especially on pyridine ring and LUMO energy is -1.956 eV. The energy gap between HOMO and LUMO is 4.076 eV, which leads the molecule becomes less stable and more reactive. The calculated energies of frontier molecular orbitals are listed in Table 6 and the frontier molecular orbitals are shown in Figure 4. The various frontier molecule orbitals of F2CNH and listed their corresponding orbital energies are in Table 6.
Table 5. The Physico-chemical properties of F2CNH| Parameters | Values |
| HOMO | -6.032 eV |
| LUMO | -1.956 eV |
| Energy gap | 4.076 eV |
| Ionization potential (IP) | 6.032 eV |
| Electron affinity (EA) | 1.956 eV |
| Electrophilicity Index (ω) | 2.562 |
| Chemical Potential (µ) | 3.994 |
| Electro negativity (χ) | -3.994 |
| Hardness (η) | -4.076 |
Figure 4.The frontier molecular orbital for F2CNH
| Occupancy | Orbital energies a.u | Orbital energies eV | Kinetic energies a.u |
| O52 | -0.289 | -7.875 | 1.618 |
| O53 | -0.286 | -7.792 | 1.516 |
| O54 | -0.278 | -7.588 | 1.735 |
| O55 | -0.263 | -7.163 | 2.213 |
| O56 | -0.221 | -6.032 | 1.591 |
| V57 | -0.071 | -1.956 | 1.666 |
| V58 | -0.045 | -1.225 | 1.639 |
| V59 | -0.041 | -1.138 | 1.582 |
| V60 | 0.022 | 6.035 | 1.581 |
| V61 | 0.025 | 0.696 | 0.94 |
UV–Vis Spectra Analysis
The nature of the electronic transitions in the observed UV-visible spectrum of the title compound F2CNH had been studied by the TD-DFT involving configuration interaction between the singly existed electronic states. The observed UV-vis spectrum was shown in Figure 5. The electronic transitions and the corresponding excitation energies were listed in Table 7. The calculated electronic transition is shown at 333 nm whereas, the experimental electronic transition observed at 360 nm. The difference in these two values may possibly be owing to solvent influence.
Figure 5.The Theoretical and Experimental UV-Visible spectra of F2CNH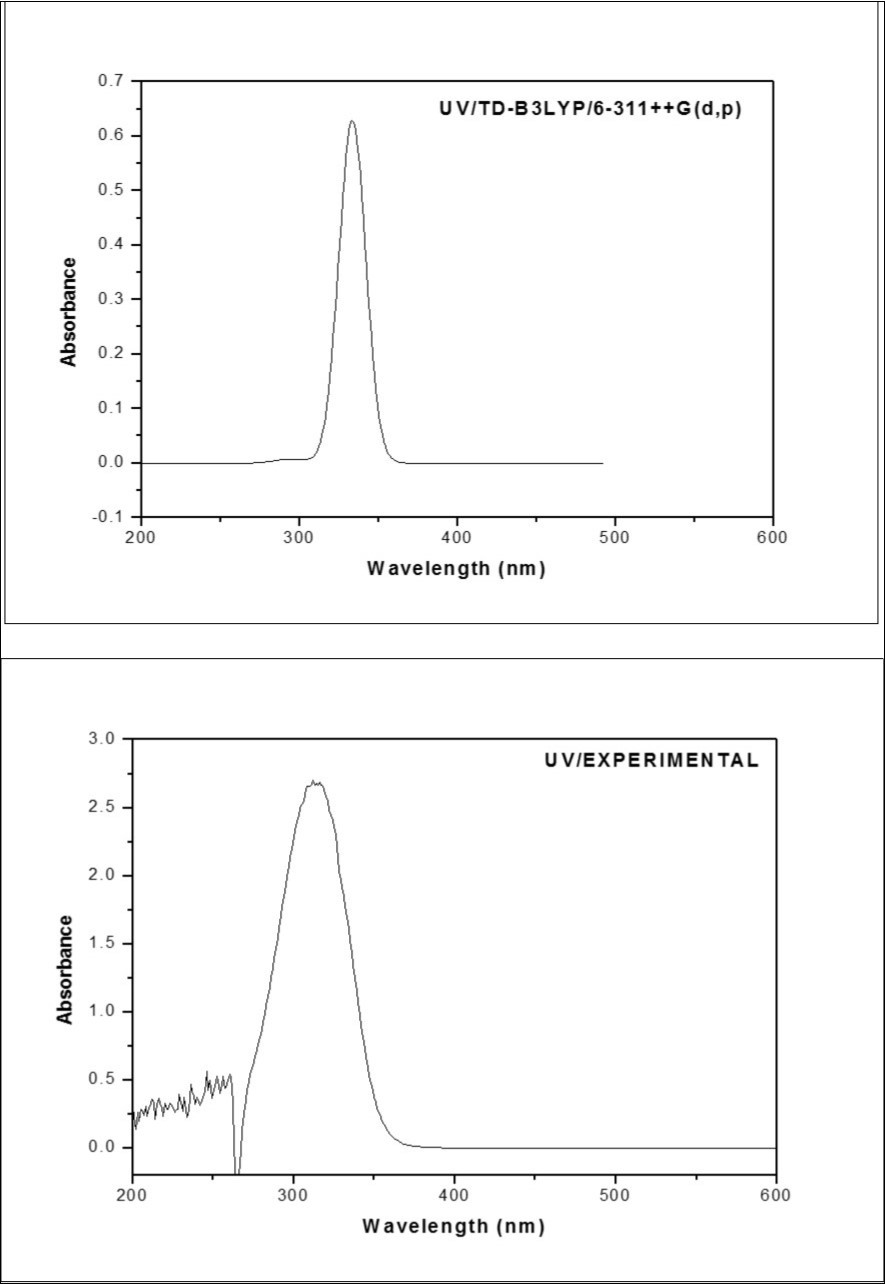
| Calculated at B3LYP/ 6-311++G(d,p) | Oscillator strength | Calculated Band gap (ev/nm) | Experimental Band gap (nm) | Type |
| Excited State 1 | Singlet-A (f=0.6299) | 3.7193 eV/333.35 nm | 360 nm | π-π* |
| 56 -> 57 | 0.6436 | 4.0763 | ||
| 56 -> 58 | 0.1052 | 4.8069 | ||
| Excited State 2 | Singlet-A (f=0.0039) | 4.1291 eV/300.27 nm | ||
| 55 -> 57 | 0.658 | 5.2074 | ||
| 55 -> 59 | -0.1462 | 6.0253 | ||
| Excited State 3 | Singlet-A (f=0.0047) | 4.2664 eV/290.61 nm | ||
| 56 -> 58 | 0.5608 | 4.8069 | ||
| 56 -> 59 | 0.4178 | 4.8942 |
MEP Analysis
The molecular electrostatic potential (MEP) map was calculated using B3LYP/6-311++G(d,p) level of basis set. The 3D plot of MEP map of F2CNH is shown in Figure 6. In MEP map, the maximum positive/negative regions are preferred sites for nucleophilic/electrophilic attack and are represented by Blue/Red colour, respectively. The importance of MEP lies in the fact that it simultaneously displays molecular size, shape as well as positive, negative and neutral electrostatic potential regions in terms of color grading Figure 6 and is very useful in research of molecular structure with its physiochemical property relationship 41, 42.
Figure 6.The Molecular electrostatic potential map of F2CNH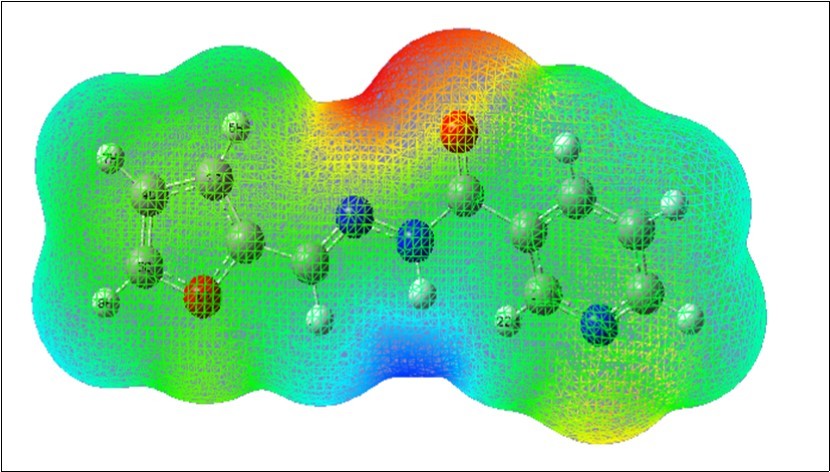
The Potential increases in the order of red < orange < yellow < green < blue. The color code of this map is in the range between -6.471 a.u. (deepest red) to 6.471 a.u. (deepest blue) in F2CNH, where blue indicates the strongest attraction and red indicates the strongest repulsion. It can be seen from the MEP map of the F2CNH, the regions having the negative potential are over the carbonyl group while the regions having the positive potential are over all the hydrogen atoms.
Mulliken Charge Analysis
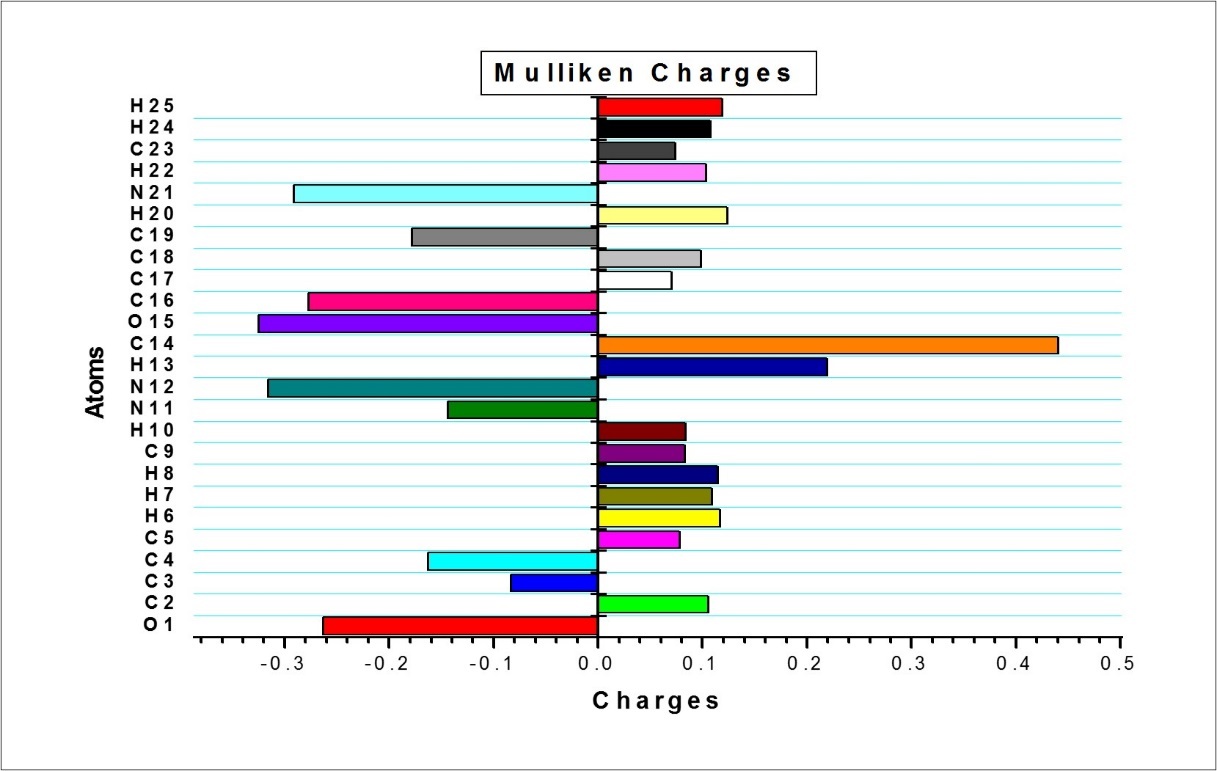
Mulliken atomic charge calculation has an important role in the application of quantum chemical calculation to molecular system, since atomic charges affect the dipole moment, molecular polarizability, electronic structure and more a lot of properties of molecular systems. The Mulliken charges were calculated by DFT/B3LYP/6-311++G(d,p) basis set. The calculated Mulliken charge values are listed in Table 8 and are plotted in Figure 7 The carbonyl group has the most positive C14: 0.440 and most negative charge O15: -0.3255 and all the hydrogen atoms have positive charge.
Table 8. The Mulliken atomic charges of F2CNH| Atoms | Charges | Atoms | Charges | Atoms | Charges |
| O1 | -0.263 | H10 | 0.0832 | C19 | -0.1788 |
| C2 | 0.1051 | N11 | -0.1439 | H20 | 0.1235 |
| C3 | -0.0835 | N12 | -0.3159 | N21 | -0.291 |
| C4 | -0.1635 | H13 | 0.2189 | H22 | 0.1033 |
| C5 | 0.0781 | C14 | 0.4399 | C23 | 0.0732 |
| H6 | 0.1163 | O15 | -0.3255 | H24 | 0.1075 |
| H7 | 0.1089 | C16 | -0.2773 | H25 | 0.1189 |
| H8 | 0.1145 | C17 | 0.0703 | ||
| C9 | 0.0824 | C18 | 0.0979 |
Thermodynamic Properties
The various thermodynamic parameters such as: total energies, zero-point energy etc were calculated using B3LYP/6-311++G(d,p) basis set are presented in Table 9. On the basis of vibrational analysis, the statistical thermodynamic functions heat capacity (C0p,m)
entropy (S0m), and enthalpy changes (ΔH0m) for the F2CNH were obtained from the theoretical harmonic frequencies listed in Table 10. It can be seen from Table 10, the thermodynamic functions are increasing with temperature ranging from 100 to 1000 K due to the fact that the molecular vibrational intensities increase with temperature. The correlation equations between heat capacity, entropy, enthalpy changes and temperatures were fitted by quadratic formulas and the corresponding fitting factors (R2) for these thermodynamic properties is 0.99895, 0.99997 and 0.99946 respectively. The comparative thermodynamical graphs of F2CNH are shown in Figure 8. The corresponding fitting equations are as follows:
C0p,m = 5.42703 + 0.02291T + 2.0243x10-5 T2 (R2 = 0.99895)
S0m = 1.24898 + 0.00527T + 4.65873x10-5 T2 (R2 = 0.99997)
ΔH0m = 3.05729 + 0.01291T + 1.14038x10-5 T2 (R2 = 0.99946)
Table 9. The calculated total energy (a.u), zero point vibrational energies (Kcal/mol), rotational constants (GHz) and entropy (cal/mol K-1) for F2CNH| Parameters | B3LYP/6-311++G(d,p) |
| Total Energies | -739.434 |
| Zero-point Energy | 117.048 (Kcal/Mol) |
| Rotational constants (GHZ) | 2.117 |
| 0.177 | |
| 0.165 | |
| Entropy | |
| Total | 119.061 |
| Translational | 42.001 |
| Rotational | 32.915 |
| Vibrational | 44.145 |
| T (K) | S (J/mol.K) | Cp (J/mol.K) | ddH (kJ/mol) |
| 100 | 341.24 | 97.36 | 6.77 |
| 200 | 425.36 | 153.35 | 19.22 |
| 298.15 | 498.26 | 216.68 | 37.35 |
| 300 | 499.6 | 217.89 | 37.75 |
| 400 | 570.98 | 279.98 | 62.71 |
| 500 | 639.27 | 332.23 | 93.41 |
| 600 | 703.68 | 374.06 | 128.81 |
| 700 | 763.94 | 407.38 | 167.94 |
| 800 | 820.16 | 434.28 | 210.07 |
| 900 | 872.62 | 456.34 | 254.64 |
| 1000 | 921.68 | 474.68 | 301.21 |
Figure 8.The thermodynamic properties at different temperatures of F2CNH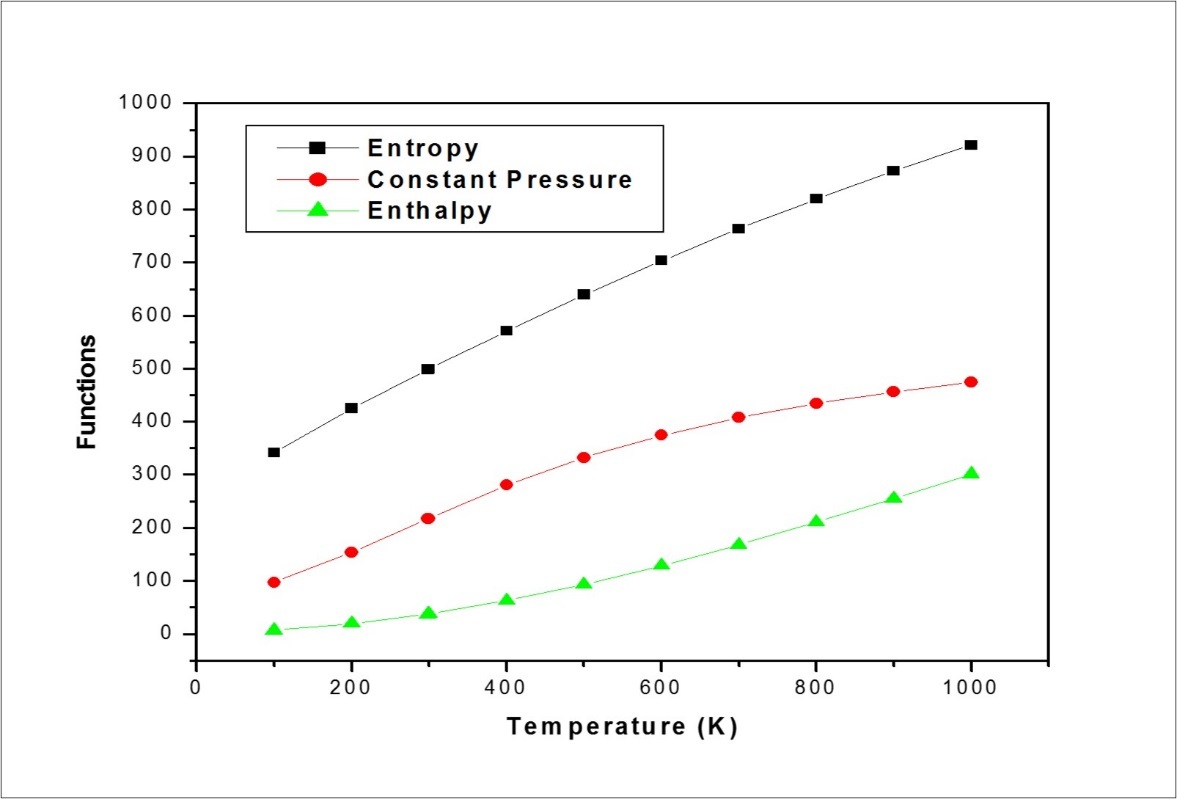
All the given thermodynamic data are the helpful information for further study on F2CNH. They can be used to compute the other thermodynamic energies according to relationships of thermodynamic functions and estimate directions of chemical reactions according to the second law of thermodynamics in thermochemical field 43. All the thermodynamic calculations were done in gas phase and they could not be used in solution.
Conclusion
A complete vibrational analysis has been carried out for the first time to the molecule F2CNH. The optimized bond parameters agree well with the literature values. The observed FT-IR, FT-Raman and UV-Vis absorption spectral values are in good agreement with the calculated values. The first order hyperpoharizability (β0=2.0918x10-30 esu) of F2CNH was calculated and found to be six times greater than that of urea and hence the molecule has considerable NLO activity. The hyperconjucative interaction π(C17-C19)→π*(N21-C23)transfer more energy 122.13 kJ/mol, which leads the ν(C23-N21) mode appeared at higher frequency (1542 cm-1) than the ν(C18-N21) mode. The Homo-Lumo energy gap was calculated about 4.076 eV. The UV-Vis study reveals that an electronic transition takes place from furan to pyridine ring via hydrazone linkage and resresented as π-π* type. MEP surface analysis mentioned the active charge sites of the molecule F2CNH. In addition Mulliken charges and thermodynamic properties are also reported.
References
- 2.L A Paquette, P C Astles. (1993) Total synthesis of furanocembranolides. 3. A concise convergent route to acerosolide. , J. Org. Chem 58, 165-169.
- 3.Forster H, Fuess H, Geidel E, Hunger B, Jobic H et al. (1999) Adsorption of pyrrole derivatives in alkali metal cation-exchanged faujasites: comparative studies by surface vibrational techniques, X-ray diffraction and temperature-programmed desorption augmented with theoretical studies Part I. Pyrrole as probe molecule. , Phys. Chem. Chem. Phys 1, 593-603.
- 4.I A Beta, Bohlig H, Dobler J, Jobic H, Geidel E et al. (2001) Adsorption of furan, 2,5-dihydrofuran and tetrahydrofuran on sodium-ion exchanged faujasites with different Si/Al ratios. Studies in Surface Science and Catalysis 218 .
- 5.Moro S, J K Chipman, J W Wegener, Hamberger C, Dekant W et al. (2012) Furan in heat-treated foods: Formation, exposure, toxicity, and aspects of risk assessment. , Mol. Nutri. and food research 56, 1197-1211.
- 6.Anese M, Manzocco L, Calligaris S, M C Nicoli. (2013) Industrially Applicable Strategies for Mitigating Acrylamide, Furan and 5-Hydroxymethylfurfural in Food,J. agri. food chem.
- 8.Waizenegger W, Atzpadin N, Schreer O, Feldmann I, Eisert P. (2012) Model based 3D gaze estimation for provision of virtual eye contact. , (ICIP-2012). Orlando Florida, USA
- 9.Bakhiya N, K E Appel. (2010) Toxicity and carcinogenicity of furan in human diet. , Archive. Toxi 84, 563-578.
- 10.Y P Kitaev, Buzykin B I, Troepol’skaya T V. (1970) The review surveys the present state of research on the conformation, isomerism, and intramolecular interactions of molecules of the immense class of organic compounds containing a hydrazone group. A list of 221 references is included. , Russ. Chem. Rev 39, 441-456.
- 11.N P Belskaya, Dehaen W, V A Bakulev. (2010) Synthesis and properties of hydrazones bearing amide, thioamide and amidine functions. , Archive. Org. Chem 275-332.
- 12.Dadiboyena S, Nefzi A. (2011) Synthesis of functionalized tetrasubstituted pyrazolyl heterocycles – a review. , Eur. J. Med. Chem 46, 5258-5257.
- 13.A M Wu, P D Senter. (2005) Arming antibodies: prospects and challenges for immune conjugates. , Nat. Biotechnol 23, 1137-1146.
- 14.Babu Ramesh, N Subashchandrabose S, M Syed Ali Padusha, Saleem H, Erdogdu Y. (2014) Synthesis and spectral characterization of hydrazone derivative of furfural using experimental and DFT methods. , Spectrochim. Acta A 120, 314-322.
- 15.Narayan Vijay, Hriday Narayan Mishra, Prasad Onkar, Sinha Leena. (2011) Electronic structure, electric moments and vibrational analysis of 5-nitro-2-furaldehyde semicarbazone:. , A D.F.T. study”, Comp. Theo. Chem 973, 20-27.
- 16.Nathiya A, Saleem H, Bharanidharan S, Suresh M, Padusha M S A. (2015) . Int.Lrs of Chem.61 162-177.
- 17.M J Frisch, G W Trucks, H B Schlegel, G E Scuseria, M A Robb et al. (2004) GaussianInc. , Wallingford, CT
- 18.H B Schlegel. (1982) Optimization of equilibrium geometries and transition structures. , J.Comput. Chem 3, 214-218.
- 22.Ravikumar C, I H Joe, V S Jayakumar. (2008) Charge transfer interactions and nonlinear optical properties of push–pull chromophore benzaldehyde phenylhydrazone: A vibrational approach. , Chem. Phy. Lett 460, 552-558.
- 24.C B Tang. (2011) 2-Methyl-N’-[1-(2-pyridyl) ethylidene] benzohydrazide, Acta Cryst. E 67: o 271–o 271.
- 25.Nair N, Sithambaresan M, Kurup M R P. (2012) N′-[(E)-(3-Fluoropyridin-2-yl) methylidene] enzohydrazide monohydrate. , Acta cryst, E 68, 2709-2709.
- 26.R M Silverstein, G C Bassler, T C Morrill. (1991) Spectrometric Identification of Organic Compounds,JohnWiley. , Chichester
- 27.Socrates G. (2001) Infrared and Raman Characteristic Group Frequencies–Tables and Charts, third ed.,Wiley,New York.
- 28.V K Rastogi, M A Palafox, R P Tanwar, Mittal L. (2002) 3,5-Difluorobenzonitrile: ab initio calculations. , FTIR and Raman spectra, Spectrochim. Acta A 58, 1987-2004.
- 29.Silverstein M, G C Basseler, Morill C. (1981) Spectrometric Identification of Organic Compounds,Wiley,NewYork.
- 30.Iliescu T, F D Irimie, Bolboaca M, Paisz Cs, Kiefer W. (2002) Vibrational spectroscopic investigations of 5-(4-fluoro-phenyl)-furan-2-carbaldehyde. , Vib. Spectrosc 29, 235-239.
- 33.Balachandran V, Santhi G, Karpagam V, Lakshmi A. (2013) DFT computation and spectroscopic analysis of N-(p-methoxybenzylidene)aniline, a potentially useful NLO material. , J. Mol. Struct 1047, 249-261.
- 34.Subramanian N, Sundaraganesan N, Jayabharathi J. (2010) Molecular structure, spectroscopic (FT-IR, FT-Raman, NMR, UV) studies and first-order molecular hyperpolarizabilities of 1,2-bis(3-methoxy-4-hydroxybenzylidene)hydrazine by density functional method. , Spectrochim. Acta A 76, 259-269.
- 35.Roeges N P G. (1994) A Guide to the Complete Interpretation of Infrared Spectra of Organic. , Structures,Wiley,New York
- 36.Barathes M, G D Nunzio, Ribet M. (1996) Polarrons or Proton transfer in chains of peptide gropus. , Synth. Met 76, 337-340.
- 37.Krishnakumar V, Muthunatesan S. (2006) FT-IR, FT-Raman spectra and scaled quantum mechanical study of 2,3-dihydroxy pyridine and 2,4-dihyroxy-3-nitropyridine, Spectrochim. , Acta A 65, 818-825.
- 39.W A Heckle, H A Ory, J M Talbert. (1961) The infrared spectra of some chlorinated derivatives of s-triazine. , Spectrochim. Acta 17, 600-606.
- 40.N Ramesh babu, Subashchandrabose S, Padusha MSA, Saleem H, Manivannan V et al. (2014) . , J.Mol. Structure 1072, 84-93.
- 41.J S Murray, Sen K. (1996) Molecular Electrostatic Potentials, Concepts and 399 Applications,Elsevier,Amsterdam.
Cited by (3)
- 1.Anizaim Ainizatul Husna, Zaini Muhamad Fikri, Razak Ibrahim Abdul, Arshad Suhana, 2021, Insight into the impact of the substituent modification on the photovoltaic performance of ferrocenyl chalcones based DSSCs, Journal of Solid State Chemistry, 304(), 122551, 10.1016/j.jssc.2021.122551
- 2.Towseef Ahmad Hajam, Mohammed Ameen K. K., Saleem H., Syed Ali Padusha M., Mashood Ahamed F. M., 2023, Molecular structure determination, spectroscopic, quantum computational studies and molecular docking of 4-(E)-[2-(benzylamino)phenylimino) methyl-2]ethoxy phenol, Journal of Biomolecular Structure and Dynamics, 41(8), 3574, 10.1080/07391102.2022.2052354
- 3.Srikanth Katta Eswar, Rao D. Jagadeeswara, Seetaramaiah V., Veeraiah A., 2019, Molecular geometry and vibrational analysis of 1-(2, 5-dimethyl-furan-3-yl)-ethanone by using density functional theory calculations, Materials Today: Proceedings, 18(), 2019, 10.1016/j.matpr.2019.06.010