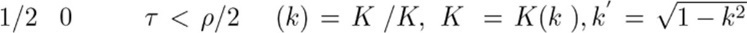Abstract
The hydrodynamic production considers the filtration of liquid from the pits, fenced with spools of Zhchukovskiy, through a layer of soil, underrunable by a well-permeable pressure aquifer, on the roof of which contains an impenetrable area. To study infiltration on the free surface of groundwater, a mixed regional multi-parametric task of the theory of analytical functions is formulated, which is solved by the Semibarinova-Kochina method and methods of conformal display of areas of special species characteristic of the tasks of underground hydromechanics. Refs. 24. Il. 4. Table 1.
Author Contributions
Academic Editor: Jayanta Das,
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2021 E. N. Bereslavsky
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
kovsky. In a number of works, free filtration was studied, i.e. the current without support, and in some cases - pressure, i.e. the presence of a free surface was neglected. In all of these studies, infiltration was not recorded. In addition, different techniques were used to solve the problems: the function of Zchukovsky and the way Vedernikov-Pavlovsky, bringing the case to the conformal display of straight polygons, followed by the use of the Kristoffel-Schwartz formula.1
As shown in the "13" way, the practical application of these methods only leads to effective results when the boundary of the area of motion consists of horizontal waterproof and vertical waterproof areas. However, in the real conditions of hydrotechnical construction (channels, reservoirs) directly under cover sediments along with horizontal aquifers of higher permeability (galeks, gravel, coarse-grained sands) are often found and horizontal waterproof areas (impenetrable inclusions, cul-de-pressure rocks), which is fundamentally reflected in the nature of filtration processes. In such situations, the use of Kristoffel-Schwartz integral does not lead to the goal, as in areas of complex flow speed there are already circular polygons that do not boil directly to the straight line.2
In contrast to these studies, the following is both a direct continuation and development of the author's previous works (see. The task of the flow of liquid from the pits through the ground array of finite power, underpowered by a well-permeable pressure aquifer containing a waterproof area on its roof, is studied, if there is infiltration on a free surface. The most common case of movement is considered, in which on both waterproof sections of the border the filtration area the flow takes extreme values and the point of zero flow speed goes to the spool (which, apparently, has not been found in the literature so far). There are extreme cases of current associated with the absence of both support, impenetrable inclusion or infiltration, and the case of degeneration of pits in the semi-endless left flooding strip, previously studied by V. V. Vedernikov. Results are provided for a diagram that occurs in the absence of critical points when the flow rate at the end of the spool is finite; the resulting solution is a certain analogue of the classic task of Zhchukovskiy.3
To solve the mixed regional multi-parametric problem, analytical function theory uses the Semibarinova-Kochina method, as well as special-species methods developed for areas of special species, which are very typical of underground hydromechanics. Taking into account the specifics and characteristics of the movement allows you to present solutions through special, and in some cases elementary functions, which makes their application simple and convenient.4
On the basis of the built accurate analytical dependencies and through numerical calculations, hydrodynamic analysis of the influence of all physical parameters of the scheme on the picture of the phenomenon is noted and some features of the models being developed are noted. The results of mathematical modeling for all marginal cases are compared to the main filtration scheme. *5
*The Work was Announced Earlier in the year.
Main model. Setting a task. The flat established current from A’A Sthe 2 l-width lpit, enclosed by symmetrical S-length sprunts, isconsidered, through a waterproof layer of T power soil with a substline aquifer E’E containing underground or artesian waters, The pressure in which has a permanent value H0 (Figure 1) On the roof of this layer is a waterproof area, D’D simulated horizontal segment length 2L. Due to thesymmetry of the motion picture, we will limit ourselves to the study of the right half of the ABCDEGR filtrationarea.6
Figure 1.A picture of the current from the pit, calculated at the e= 0.6, T = 7, S = 3, H0 = 3, L = 15, H = 4, l = 10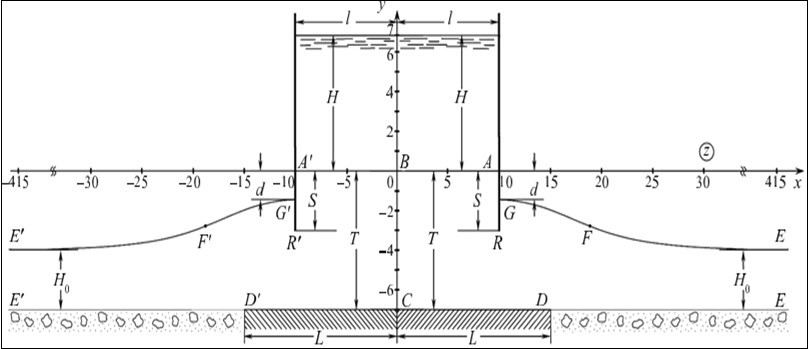
Groundwater, dflowing ARG spool under the influence of pressure difference in the pit and the underlying well-permeable aquifer, rise behind it to a certain height of the RG and, overcoming the point of M zero speed on the spool, form a free surface of GE ,which receives infiltration waters with the intensity of the e (0<e< 1),attributed to the ground filtration factor of the k= const. .7
We will assume that the movement of groundwater is subject to the law of Darcy with a known filtration factor of z and occurs in a homogeneous and isotropic soil, which is considered incompressible.8
Under such conditions, as it is known, the basic fluid filtration equations can be recorded as
 ….(1)
….(1)
Where φ is the potential for filtration speed; u and v - projections on the axis of filtration rate coordinates; h - pressure; p - pressure in the stream; γ is the specific weight of the liquid 9
From a mathematical point of view, the challenge is to find the complex potential of the flow of z (φ the potential of speed, ψ is the function of the current) as an analytical within the filtration area of the function of the complex coordinates z under the following boundary conditions:10
AB : y = 0, φ = −H; BC : x = 0, ψ = 0;
CD : y = −T, ψ = 0; AG : x = l, ψ = Q; ….(2)
DE : y = −T, φ = −H0; GE : φ = −y − T, ψ = Q + ε(x − l),
The study is carried out in terms of the values of z and ω which are related to the actual values of the same through the means of equality.11
 .
.
Building a solution to the edge problem. Let's turn to the area of complex velocity w (Figure 2) corresponding to the edge conditions (2). This area, which is a circular polygon with three incisions, tops N1 and N2 two of which correspond to the extremes of current function on impenetrable areas of AB and DE, belongs to the class of polygons in the polar grids. However, unlike the "15" limit, an additional corner point appears on the boundary of the traffic area, point B (see Figure 1); the total number of special points becomes nine, making the task much more difficult.12
Figure 2.Complex W speed area for the main filtration scheme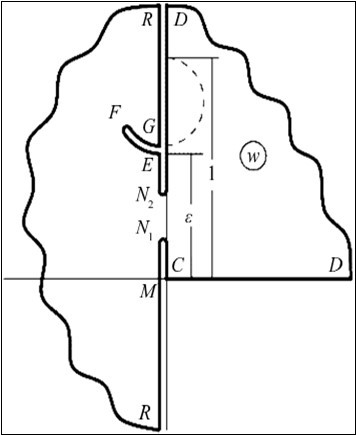
To solve the regional problem, the Semibarin-Kochina method, which is based on the application of the analytical theory of linear differential equations of the Fuchs class. Entered
Auxiliary parametric variable ζ and z functions : conformally displaying the upper half-flatness on the z area when dots are matched 13
ζE = 0, ζG = 1, ζC = k−2 (0 < k < 1), ζD= ∞,
as well as derivatives
 .
.
By determining the characteristic performance of the functions of the and the "regular special points" near the regular special points, we will find that they are linear combinations of the two branches of the next function of Riemann.14
 ….(3)
….(3)
It can be seen that the points ζ = ζA and ζ= ζBare the common points of function Y, representing the last symbol of Riemann, which corresponds to the linear differential equation of the Fuchs class with seven regular special points, very typical for the tasks of underground hydromechanics.15
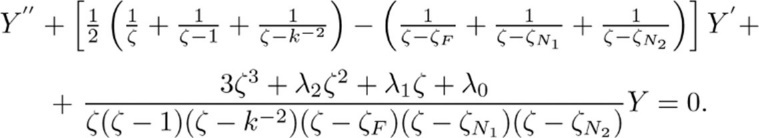 …..(4)
…..(4)
Recall that along with ζ the ζF, ζN1 and ζN2 in the equation (4) the accessory parameters of0,λ1 and 2remain unknown in setting the task and must be determined in the course of its solution.
Replacing variables
ζ = sn2(2Kτ,k)…(5)
translates the upper half-flatness ζ into a rectangle of the plane:
I'm where , ρK(k) is a full elliptical integral of the first kind with module ( k, 23, when dots are matched
τE = 0, τG = 1/2, τC = (1 + iρ)/2, τD = iρ/2,
and the Y equation integrals (4), which correspond to the symbol of Riemann (3) and are constructed according to the technique developed earlier, are transformed as follows:
Y1,2(τ) = θ0−3(τ)θ1(τ ± iγ)θ2(τ ± iβ)θ2(τ * iβ)exp(±iπτ). (6)
Here, sn τ = sn (u.k) is Jacobi's elliptical function (sinus) at module k, θ1((q),θ0((q) - theta function with the parameter q q exp, which is uniquely associated with the module k , q, γ - some suitable permanent.16
Taking into account the ratios (3), (5) and (6), as well as the fact that the functionshas the same appearance.
 ...(7)
...(7)
√ε = thπ(ρ/2 + β − α − γ), ..(8)
come to the addictions we're in.
 ….(9)
….(9)
in which N is a large-scale constant simulation, sn- unknown residents of points A and B of the area of q.
(9) Permanent conformal displays of q, z and γ, which are bound by a ratio (8), are subject to the conditions
0 < α < r < β < m < a < b < ρ/2, 0 < γ < ρ/2,...(10)
Regulating the position on the boundary of the flow of points M and point of the spun R, as well as N1 and N2;; m and r are unknown residents of M and R points in the plane. τ.
You can verify that the functions (9) meet the conditions (2) reformulated in terms of functions, and thus are a parametric solution to the original edge problem.17
Recording ratios (9) for different parts of the boundary of the area, followed by integration across the entire loop of the auxiliary area, leading to a close of the movement area and thus serves as a control of the calculations.18
 ….(11)
….(11)
 ….(12)
….(12)
and coordinates of the EG depression curve points
 ….(13)
….(13)
Account control is other expressions for the values d,L and filtration expense::
 ….(14)
….(14)
In formulas (11)-(14) subtegrial functions are expressions of the right parts of equality (9) on the corresponding sections of the contour of theregion.19
Analysis of numerical results for the main filtration model. Views (9) --(14) contain seven unknown permanents: residency prototypes of points A,B,R in the plane τq , parameters of conformal display, γ, satisfying ratio (8) and inequities (10), as well as module k (0 < k < 1) and constant N modeling. N
The first means that the speed at the end of the spool turns into infinity, and the second is directly derived from the consideration of boundary conditions (2). After determining the unknown permanents are the exact values d and z by expressions (12) and finally, the formulas (13) are calculated coordinates of the points of the free surface EG.20
On rice. 1 is a picture of the current, calculated at q= 0. 6, To= 7,S,H= 3,H 3,L= 15,H, = 7L, 10 (basic values). and the rest are fixed by the baseline values, the results of calculations of the influence of the determining physical parameters are 0,T,S,H and L on the depth of D (negative values d means that the free surface rises above the absiss axis) and the expense of the q. Figure 3 are represented by the dependence of the d and filtration consumption of the 0,T,H,H,H,H.L.H. ε,T,S,H0,L,H,l.21
Figure 3.Dependencies of values d (1) and q (2) from different parameters (a - from the T at 7, S 3, H0, 3, L, 15, H, 7, l q 10; b - from T at H 0.6, S 3, H 0, L, L, 15, H, 7, l q 10; in - from S at 0.6, T 0.6, T 7, H 0, 3, L, 15, H, 7, L q 10; g - from H0 at 0.6, T q 7, S 3, L q 15, H q 7, l q 10; d - from L at 0.6, T q 7, S 3, H0, 3, H, 7, l q 10; e - from H at 0.6, T q 7, S, 3, H0, 3, L, 15, l q 10; f - from l at q 0.6, T q 7, S 3, H0, L q 15, H q 7.
Analysis of table and rice data. 3, and allows you to draw the following conclusions.
First of all, the same quality of dependencies of the values H ,L,d,S and l, associated with a decrease Q infiltration intensity and greater reservoir power, in which these filtration characteristics grow. 22
Increase infiltration intensity, impenetrable inclusion and pressure in the underlying layer and reduce the power of the layer, The length of the spool, the d pressure of the water in the pit ε,S,H and its width lead to a drop in the depth d,i.e. to the increase of the residents of the point G exit of the depression curve from under the spool. 23. Table 1.
Table 1.| Ε | D | Q | T | D | Q | S | D | Q | H0 | D | Q |
| 0.5 | 2.651 | 0.182 | 6.5 | 1.349 | 0.234 | 2.0 | 1.726 | 0.635 | 2.0 | 3.155 | 0.038 |
| 0.6 | 1.804 | 0.394 | 7.0 | 1.804 | 0.394 | 2.5 | 1.745 | 0.563 | 4.0 | 0.441 | 0.769 |
| 0.7 | 0.586 | 0.457 | 7.5 | 2.299 | 0.457 | 3.5 | 1.844 | 0.255 | 5.0 | –0.93 | 1.159 |
| 0.8 | –1.195 | 0.094 | 8.0 | 2.745 | 0.627 | 4.0 | 1.873 | 0.129 | 6.0 | –2.35 | 1.815 |
The results of the calculations of D and Z values However, the greatest impact on the depth of D is an impenetrable area: table data show that when L width increases by only 28%, the depth d increases by almost 10 times.
Atd) = ( –d)/S, h(S) = 0 h( ε,T,S,H0,L,H,lH 0.8, H0and 5 and L and L 18,i.e. at fairly large parameters, H,H0 and L, the free surface rises above the abscissus axis, with the values d negative. Table 2.
Table 2.| L | D | Q | H | D | Q | L | D | Q |
| 14 | 2.555 | 0.086 | 4.0 | 0.650 | 1.815 | 10.0 | 1.804 | 0.394 |
| 16 | 1.116 | 0.599 | 5.0 | 1.070 | 1.159 | 10.3 | 2.018 | 0.320 |
| 17 | 0.413 | 0.888 | 6.0 | 1.441 | 0.769 | 10.6 | 2.229 | 0.253 |
| 18 | –0.256 | 1.084 | 8.0 | 2.155 | 0.038 | 11.0 | 2.478 | 0.230 |
characterizing the relative elevation of groundwater behind the spool, ε,H we receive h–(-1).. ( 1945) = 1. 3981, h(–0. 9297) = 1. 3099, h(–2. 3500) = 1. 7833 and h(-0. 2560) = 1. 0853, with the parameter hgrows with T,H0 an increase in the residents of point G exit of the depression curve from under the spool. 24
As for the flow, the larger the width of the impenetrable inclusion, the more significant the difference in the value of theq : from the table it follows that when the L parameter grows by 1.28 times the expense increases by more than 12 times.
This behavior of consumption is clearly seen both with the increase in the power of the layer, the width of the pit and the pressure in the underlying horizon, and with the decrease in the length of the spool and the pressure in the beef. It follows from the table that the reduction of the H parameter by only 2 times is accompanied by an increase in consumption of almost 48 times, which indicates the greatest impact on the pressure of water in the pit.
Limit cases. 1. Case H0 q 0. We will focus primarily on the absence of backup, i.e. movement at H0 q 0. . The solution for it is derived from dependencies (9)-(14) at the γ γ γ* * 0. At this value of theγ circular incision of the EG area w, transforming, transforming, degenerates into the right semicircle (bar line on F Figure 2), and thus the original area becomes a circular hexagon, which falls the right part of the semicircle . w−i(1+ε)/2| (1−ε)/2In the z current plane at the γ γ * the depression curve is rinsed at E point, E with which its inflection point F merges, and overlooks the roof of the underlying horizon at right angles.
Note that for q 0. 7,T 6 and 6.. 5, S q 3, L q 15, H q 5 and l q 10, in which the value of D becomes negative, the H is 1.2191, 1.2020, 1.0140, 1.0443, 1.0638 and 1.0442 respectively.
Case = 1
Z’ = Z+l bρ/2 Abbl ∞. Consider the case where the width of * ∞ * the pitincreases indefinitely. so that the filtration area becomes a semi-endless flooding band on * the left.
In = 0themain filtration scheme discussed above, the absence of such a powerful factor as impenetrable inclusion, being the limit, serves as a backdrop to assess the role of infiltration and pressure in the underlying layer and allows for a more contrasting response to the interaction of such important physical parameters as q and H0..
If there is no impenetrable area on the roof of the underlying aquifer, the latter becomes well permeable all along. When 1/2Im Re DC and D points merge in the area of complex speed, Cw, its left semi-flatness is cut off, The circular incision of the EG goes into the right half-flatness, and the original area is transformed into a ∞ circular triangle.
 .
.
The solution for this extreme case is derived from formulas (9)-(14), if they put k q 0 and take into account that in this case elliptical functions degenerate into trigonometry, and theta functions break off on their first members or constants:
 ,…..(15)
,…..(15)
where
There are prototypes of M,R,C points on the absciss of the plane. τ.
 case of = 0 L, we will focus on the absenceof infiltration.
case of = 0 L, we will focus on the absenceof infiltration.
Thus, it turns out to solve the problem, first considered by V. V. Vedernikov, only in another way.
A case of the final speed of the flow at the end of the spool. As part of the edge task (2), consider the case where the flow rate at the end of the spool vR, < ε 0 qlt; Then in the area of complex speed w both vertical incisions disappear, the left half-flat is cut off, as before at L q 0,however, unlike the latter, the MR section is transferred to the first quadrant.
The parametric solution of the problem formally has the same form (9) with the replacement of integrals Y1,2((q) and permanent conformal display of q and q for the following:
Y1,2(τ) = θ−01(τ)θ1(τ ± iγ)exp(±iπτ),…(16)
α = β = (1 + iρ)/2...(17)
The solution to a similar problem in the absence of backup arises from submissions (9), (16), (17) at γ of γ*.
Analysis of the numerical results shows that in vRqlt; ∞ the qualitative nature of filtering dependence on the physical parameters of the scheme is maintained, characteristic of the case vR ∞. For example, there is the same as before, the pattern of flow behavior from values T and l, on theone hand, and contrary to the parameters of S and H - on the other.
On rice. 4 is a picture of the movement, calculated at the z 0. 5, T = 6, S = 3, H0 = 0, L = 16. 2, H = 3. 8, l = 15. It is noteworthy that for all the calculated variants 1) of d'S and therefore h(d)h(s) q 0. This means that in the current plane point G exit of the depression curve from under the spool merges with the point R of its edge; from the consideration of the area of complex speed w it follows that in this case the speed at the end of the spint is equal to the intensity of the infiltration: vrq(Figure 4).
Figure 4.The current pattern in the case of v ε R, calculated at 0.5, T q 6, S 3, H0 q 0, L = 16.2, H = 3.8, l = 15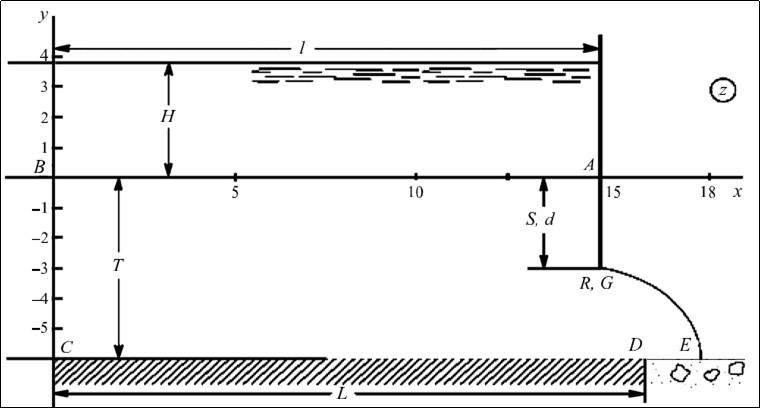
If you make a transformation T’ =1/2+iᑭ’t hat translates a rectangle of auxiliary variables to a similar one to the parameter, then the corresponding basicᑭ’ = 1/ᑭ = K/K’ filtering scheme of the inequality to the parameters (10) will take the form
0<b’<α’<r’<1/2,
Where b’,α’<r’ there are abscisses of B,A,R points in the plane.
Calculations show that for any infiltration intensity, the d > S, ratio of d s is only for r’* a single r - its limit- when the G HR: r’ = r*’=1/2plane r’ <r’*is merged.
Such a result in the marginal case for the model in question, when the waterproof layer of soil has unlimited power, there is no impenetrable site and infiltration, i.e. at the time of
1 And ε=0(m’ = 0), was first received by N. E. Schukovsky. 
и учесть, что при этом
2 The functions degenerate into hyperbolic, and theta functions, which this time are characterized by theq’=0 parameter, break off on their first members or constants.
3 Thus, in the extreme case of the scheme studied, it turns out to solve the problem of Shchukovsky, but only in a different way.
4 The author thanks the reviewers for helpful tips and comments that contributed to the improvement of the work.
References
- 1.Vedernikov. (1935) Effect of capillary uplift on filtration from channels / Hydrotechnical construction. 5, 20-27.
- 2.Vedernikov. (1936) Effect of soil capillary on filtration with a free surface /. , Dock. Ussr. T 3(4), 157-161.
- 3.V I Aravin.Inflow of groundwater to the pit, fenced with spools /. , Izv. All-union. study. 1937. T 20, 74-89.
- 4.V S Kozlov. (1939) Hydromechanical calculation of spool jumpers / Izv. AN USSR. It's not a good one. Technical. Sciences 6, 89-110.
- 5.Vedernikov. (1939) Theory of filtration and its application in the field of irrigation and drainage. , M.; L.: Gosstroyizdat 248, s..
- 6.Nelson-Skornyakov F B. (1943) Hydromechanical calculation of water flow to the pit / Izv. AN USSR. It's not a good one. , Technical. Sciences 7, 90-94.
- 7.F B Nelson-Skornyakov. (1944) Some cases of groundwater flowing from the river to the quarry (pit) / Izv. AN USSR. It's not a good one. Technical. Sciences 3, 209-220.
- 8.F B Nelson-Skornyakov. (1949) Filtering in a homogeneous environment. 2nd. ed. M.: Soviet science 568.
- 9.V I Aravin, Numerov S N. (1948) Filtering calculations of hydraulic facilities. , M.: Stroyizdat 616, s..
- 10.Vederniks. (1949) Filtering in the presence of a drainage or aquifer /. , Dock. Ussr. T 69(5), 619-622.
- 11.L D Apothecary.Issues of filtration calculation of horizontal drainage of navigable gateways and dry docks -. , Izv. All-union. study. 1951. T. 46. S 80-105.
- 13.Science P J Polubarinova-Cochina M. (1969) Development of research on the theory of filtration in the USSR. 546.
- 15.E N Bereslavsky. (2013) About some hydrodynamic models related to the task of Schukovsky about the streamlining of the spool. , T 448(5), 529-533.
- 16.Bereslavsky E N, Cochina P Y. (1992) About some equations of the Fuchs class in hydro and aeromechanics // Izv. AN USSR. Fluid and gas mechanics. 5, 3-7.
- 17.E N Bereslavsky, P Y Cochina. (1997) About the differential equations of the Fuchs class, which are found in some tasks of fluid and gas mechanics // Izv. AN USSR. Fluid and gas mechanics. 5, 9-17.
- 18.P J Cochina, E N Bereslavsky, Cochina N. (1996) Analytical theory of linear differential equations of the Fuchs class and some tasks of underground hydromechanics. preprint No. 567. M.: , Ch 1, 112.
- 19.E N Bereslavsky. (1980) On conformation display of some circular polygons on a rectangle /. , Izv. Universities. Mathematics 5, 3-7.
- 20.E N Bereslav. (1997) About differential equations of the Fuchs class associated with the conformal display of circular polygons in polar grids / Differenz. Equation. , T 33(3), 296-301.
- 21.E N Bereslav. (2012) About some differential equations of the Fuchs class found in the mechanics of liquids and gases // The different. Equation. , T 48(4), 590-594.
- 22.Bereslavsky E N. (2014) Application of the Method Polubarynova-Kochina to study filtration currents from pits fenced with spools of Shchukovskiy /. , Dock. Wounds. T 455(6), 651-655.