Author Contributions
Academic Editor: Abubaker Haroun Mohamed Adam, Department of Crop Science (Agronomy), College of Agriculture, Bahri University- Alkadaru- Khartoum -Sudan.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2021 Prem Narain
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
In my article, Scientific and Technological Interventions for Attaining Precision in Plant Genetics and Breeding, published on March 30 2018 7, I had reviewed the development since Mendel’s discovery of genetic laws, in terms of cloning technology and reverse genetics, chip technology, genetically modified organisms and CRISPR-based gene editing technology, in particular their roles in further refining plant genetics and breeding practices.
It is well known how statistics entered in genetics due to work of Fisher 2 when he decomposed the phenotypic variability into variability due to additive effects of genes and that due to environmental effects paving the way for the role of heritability (proportion of the former due to that by additive effects of genes) with symbol h2.
Soon after the introduction of chip technology – the genotyping of molecular markers – the method of plant breeding got a big impetus in increasing precision in the breeding process by incorporating the marker information in the methods of selection and cross breeding. The position of markers in the genome is fully known through linkage maps. With this information the methods of quantitative genetics got modified in that the variability due to additive effects of genes got further decomposed into that due to association of marker information with the genes controlling the trait and the rest. The proportion of additive genetic variability due to such association gives rise to another parameter p in addition to h2. The expression ph2 then refers to the proportion of phenotypic variation due to marker/markers information in the genome. This fraction becomes just h2when markers are totally linked with the genes controlling the trait. But when the markers are not at all associated with the genes for the trait, p becoming zero, this becomes zero. The difference (h2– ph2) is then referred to as missing heritability. In several genome-wide association studies (GWAS), genes have been identified associated with diseases but they explain only a small fraction of the variability leading to the frequently asked question of missing heritability4. For most of the economic traits in plants and animals, heritability is usually small, making missing heritability inevitable.
It shows that the missing heritability occurs because of a certain proportion of additive genetic variance not being associated with the markers. When millions of SNPs are considered in a GWAS study it is implicit that numerous QTLs causing variation in the trait are either sitting on a subset of SNPs or else are very close to them. Identification of causal variants by sparse regression methods is then an attempt to detect and locate genes responsible for the trait in terms of the SNP markers 6. The association between the SNP markers and the trait estimated this way could then be due to imperfect association between the markers and the underlying QTLs leading to what is being termed as missing heritability phenomenon. It needs to be emphasized that linkage disequilibria of various orders between the markers and the QTLs are playing their roles in generating this phenomenon. Due to complexity however such disequilibria cannot be incorporated in the analysis. However if we consider, as in plant breeding, F1, F2, F3 etc. populations derived from crossing two pure parental lines with iso-directional distribution of each of the two alleles at several loci, the gene frequencies at each of the QTL and marker loci become ½. When QTLs are sitting on the markers themselves, the recombination values between them become zero which makes the LDs of the first order to become ¼ each and LDs of higher orders to become zero. Such a contingency leads to unit value of p and missing heritability therefore to zero. With random mating populations with unequal gene frequencies such a simplification does not seem possible.
If we denote missing heritability by h2(missing) we can express the relationship as per unit of h2 giving
h 2 (missing)/h 2 = (1-p)
This is a function of p only. We can also call p as the predictability of the additive genetic effects by the molecular scores due to their association with the phenotypes via the underlying QTLs. We can then recast it as
Missing heritability = heritability – heritability *predictability.
The missing heritability depends on two parameters – the heritability h2 itself and the fraction of additive genetic variation due to association of the trait with molecular markers, denoted by p. We now plot the missing heritability as a function of these two parameters. Figure 1 illustrates this behaviour for four values of h2=0.5 (Series 4), 0.25 (Series 3), 0.2 (Series 2) and 0.05 (Series 5), with variation in p between 0 and 1. It is apparent that the missing heritability becomes smaller and smaller as p increases from 0 to 1 and that this decrease is even smaller at a lower value of h2. Table 1 gives the corresponding values of Missing Heritability at different values of heritability (h2). Table 2
Table 1. Missing Heritability at different values of heritability (h2)| p | h2 =0.05 | h2=0.20 | h2=0.25 | h2=0.5 |
| 0 | 0.05 | 0.2 | 0.25 | 0.5 |
| 0.1 | 0.0495 | 0.198 | 0.2475 | 0.495 |
| 0.2 | 0.048 | 0.192 | 0.24 | 0.48 |
| 0.3 | 0.0455 | 0.182 | 0.2275 | 0.455 |
| 0.4 | 0.042 | 0.168 | 0.21 | 0.42 |
| 0.5 | 0.0375 | 0.15 | 0.1875 | 0.375 |
| 0.6 | 0.032 | 0.128 | 0.16 | 0.32 |
| 0.7 | 0.0255 | 0.102 | 0.1275 | 0.255 |
| 0.8 | 0.018 | 0.072 | 0.09 | 0.18 |
| 0.9 | 0.0095 | 0.038 | 0.0475 | 0.095 |
| 1.0 | 0.0 | 0.0 .0. | 0.0 | 0.0 |
Figure 1.Behaviour of Missing Heritability
| (r A /r m )=1 | (r A /r m )=0.5 | (rA/rm)=0.2 | ||||
| p | 0.05 | -0.05 | 0.1 | -0.1 | 0.0 | 0.0 |
| 0.0 | 0.05 | -0.05 | 0.1 | -0.1 | 0.0 | 0.0 |
| 0.1 | 0.049 | -0.049 | 0.099 | -0.099 | 0.0001 | -0.0001 |
| 0.2 | 0.046 | -0.046 | 0.096 | -0.096 | 0.004 | -0.004 |
| 0.3 | 0.041 | -0.041 | 0.091 | -0.091 | 0.009 | -0.009 |
| 0.4 | 0.034 | -0.034 | 0.084 | -0.084 | 0.016 | -0.016 |
| 0.5 | 0.025 | -0.025 | 0.075 | -0.075 | 0.025 | -0.025 |
| 0.6 | 0.014 | -0.014 | 0.064 | -0.064 | 0.036 | -0.036 |
| 0.7 | 0.001 | -0.001 | 0.051 | -0.051 | 0.049 | -0.049 |
| 0.8 | 0.031 | -0.031 | 0.019 | -0.019 | 0.081 | -0.081 |
| 0.9 | 0.014 | -0.014 | 0.036 | -0.036 | 0.064 | -0.064 |
| 1.0 | 0.05 | -0.05 | 0.0 | 0.0 | 0.1 | -0.1 |
The above missing heritability concept has also been dealt with by de los Campos et al. 1 and Gianola et al 3 as well as the results given here are implicit in the derivations given in the Appendix of Narain 5.
When we have more than one trait under study the pair-wise correlation between the traits at the genetic level becomes crucial in addition to the heritability of the traits. Such correlations can arise from two different causes. The traits may be affected by two sets of genes, the members of which are, to some extent, linked with one another. Such correlations could, however, be transient in that their signs could be reversed or whose magnitude could be brought down to zero by breaking linkages between gene complexes by selection. The other and the most important of cause of genetic correlation is the pleiotropic effects of genes , that is, the genes concerned have a direct physiological effect on the two characters. Such correlations are of permanent type so that if a pleiotropic gene is segregating in the population it causes simultaneous variation in several characters it affects. Apart from genetic causes the correlation between two characters could be purely due to environment in that the two characters are influenced by the same differences of environmental conditions. The correlation between two characters that we observe, known as phenotypic correlation, is thus the result of both the genetic as well as environmental causes. Analogues to the partitioning of phenotypic variance into additive genetic and the rest of the variation, we have the partitioning of the phenotypic covariance, between characters 1 and 2, into additive genetic covariance, and the rest of the covariance between the traits.
The phenotypic correlation (rP)is then related to additive genetic correlation (rA)and environmental correlation. Full details can be found in Narain 8. The crucial term is rAh1h2 which is often referred to as the co-heritability between the two traits. The availability of information on molecular markers in terms of their genotypes alters this conceptual frame work. With two correlated traits, analogous to the partitioning of covariance into additive genetic covarianceand environmental covariance, we have the partitioning of the covariance between the molecular scores of the two traits and the covariance between the remainder of the additive genetic effects not associated with the markers for the two traits. The additive genetic correlation (rA) is then related to (rM), the component of the additive genetic correlation associated with the markers (molecular genetic correlation) and the component not associated with themarkers.
It may be noted that when p1=p2=1, rA =rM , the entire additive genetic correlation between the traits is associated with the markers whereas when the p’s are close to zero, the additive genetic correlations are not associated with the markers at all.
It is straightforward to see that the magnitude of imperfect association with the markers in so far as the additive genetic correlation between the traits is concerned can be seen by considering the difference between the additive genetic covariance and the covariance between the molecular markers. This shows that with p’s approaching unity this covariance component will approach zero, rAand rM becoming equal. On the other hand with p’s approaching zero this component is the additive genetic correlation times the product of the square-roots of the two heritability, or in other words, the co-heritability between the traits, setting the upper limit of the component.
We therefore find that the imperfect association of genes for the trait with the markers not only give rise to missing heritability of the traits but also the missing covariance between the traits when more than one trait is considered. We can also call it as missing co-heritability. It is apparent that with several traits we have a set of missing genetic parameters, there being k(k+1)/2 of them with k traits.
There is however one difference between missing heritability and missing co-heritability. The former is necessarily positive but the latter can be negative.
We can thus express the missing co-heritability per unit of rAh1h2, the co-heritability, as Missing Co-heritability /Co-heritability = [1 –(rM / rA)p1 p2].
It seems the expression rMh1 h2p1 p2can also be called as co-predictability of the two traits given the co-heritability of the two traits. The additive genetic effects of one trait say X is predictable by the molecular scores of the other trait say Y as well as the additive genetic effects of trait Y is predictable by the molecular scores of trait X. Then we have Missing Co-heritability = Co-heritability – Z
Z = [hx2hy2]1/2 * Co-predictability
For a numerical study, we take h1=h2=h and p1=p2=p leading to
Co-heritability (missing) = rm h2 [(rA / rm) – p2].
We plot this for h2=0.5, (rA /rm)=1, 0.5, 0.2 and rm = 0.2, -0.2, to get Figure 2.
Figure 2.Behaviour of Missing Co-heritability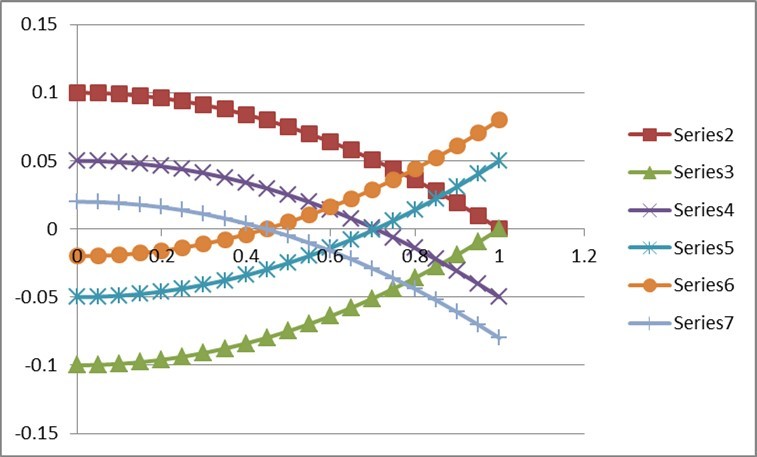
This Figure illustrates the behaviour for variation in p between 0 and 1 when rA /rm=1 in Series 2(rm=0.2) and Series 3(rm=-0.2), rA /rm =0.5 in Series 4(rm=0.2) and Series 5(rm=-0.2), rA/rm = 0.2 in Series 6(rm=0.2) and Series 7(rm=-0.2). It is apparent that missing co-heritability can be positive as well as negative unlike missing heritability which is always positive. For positive value of rm it decreases from p=0 to p=1 but for being a mirror image of the former. It is interesting to see that these curves cut the x-axis at values of p equal to the square-root of (rA/rm) as it should since missing co-heritability becomes zero at such values. These cut-off points are, respectively, 1, 0.71, and 0.45 corresponding to (rA/rm) = 1, 0.5 and 0.2. It may also be worthwhile to note that the three choices (rA/rm) = 1, 0.5 and 0.2 correspond respectively to rA = 0.2, 0.1 and 0.04.
With two traits having heritability h12 and h22, p1 and p2 as the corresponding proportions of additive genetic variances associated with the markers, rA and rM as the additive genetic and molecular correlations, there are three missing quantities depending on these six parameters, the missing heritability h12(m) and h22(m) and missing co-heritabilitycoh2(m). Is it possible to combine them into a single quantity? We have explored this aspect in 8 with necessary derivations using the principle of canonical correlation between the two sets of genetic and phenotypic values of the characters but avoid giving results here. The conclusions are given below.
The behaviour of GHmissing (missing Generalised Heritability)with variation in p isindependent of the effect of molecular genetic correlation (rm) and is practically dependent on p, for a given value of GH which means for given values of h2, rP, and rA, in almost the same manner as in the case when we consider a single trait. In other words,
h2missing = h2 (1-p2) and GHmissing = GH (1-p2)
where GH, the Generalised Heritability, for equal heritability of the two traits, is
GH = h2 [(1-rA2)/(1- rP2)]1/2.
References
- 1.De los Campos, D Sorensen G, Gianola D.Genomic heritability: what is it?. , PLOS Genet 11, 1005048.
- 2.R A Fisher.The correlation between relatives under the supposition of Mendelian inheritance. , Trans. Royal Soc., Edinburgh 52, 399-413.
