Abstract
The solution of a genetic-mathematical problem of interaction of the human population cells and virus population to a problem of pandemic COVID-19 is submitted. The mathematical model based on the Hardy - Weinberg law consisting of two interdependent differential equations is used. The equations reflect time dynamics of the human cells and virus populations during their interaction. Solutions of the differential equations are found and results of these solutions are analyzed. The estimation of duration pandemic is received at use of parameters of the human liver cells and a flu virus.
Author Contributions
Academic Editor: Yu Xiong, Associate Professor Vice presedent of Chongqing Association of Prosthodontics, China.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2020 A.N. Volobuev
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
Occurrence in the world of the pandemic COVID-19 has put a number of scientific and technical problems. First of all it is a practical problem of creation of a vaccine against of coronavirus. Does not cause doubt that this problem will be successfully solved in the near future since for creation of a vaccine the many science laboratories in the advanced countries work, and sufficient finance for researches are allocated.
However there were also other problems. In particular there is interest the forecast as a long time can last the pandemic, what global consequences will arise owing to propagation of disease. Not applying for exhaustive answers to the given questions, we shall notice that the problem of definition of the pandemic duration can be in part solved on the basis of genetic-mathematical modeling process of the two population interaction: human and virus.
First of all we shall note that the virus population cooperates not with a human population as set of very complex organisms, and with a population of separate cells of an organism. The death of the person at virus attack is exclusive enough event though on death rate estimate propagation for example of coronavirus infections, success of counteraction to it.
As a result of interaction of a virus and aт organism cell the cell can be perish that usually does not result to death of an organism as a whole. During interaction there can be perish a virus owing to functioning immune system of the person, occurrence of antibodies to a virus antigene.
At modeling a problem of a virus and an organism cell interaction arises two problems. First, it is necessary is genetically proved to model influence of the first population (human or is more exact cellular) on the second population (virus) and the second population on the first. Naturally these influences can be carried out under different laws. Second, it is necessary to take into account a various time scale for both populations since average time of a life of the human cells can differ from average time of a life of viruses essentially. These factors do the solution of a problem of the populations interaction enough complex.
Hardy – Weinberg law for cooperating populations
If there is some mutagen factor D2,1 working from the second population on first population the law of Hardy - Weinberg for the first population it is possible to write down as 1, 2:
 .......(1)
.......(1)
Where q f1 there is frequency of recessive female allele of the first population subjected to influence from the second population. As the first population we consider cells of the person organism for example cells of a liver. Dimensionless time n1=t/T1 , where T1 - average time of a life of organism cells for an individual of the first population. For cells of a liver on different sources is T1 ≈ 140days 3, 4, 5.
The Hardy - Weinberg law for the second population we shall write down similarly:
 ......(2)
......(2)
At writing of the equation (2) we have assumed that in the second population there is no division into male and female individuals, so Q2 there is a frequency of recessive allele which is subjected to influence in genome of the second population. For example, such situation is characteristic for bacterial, microbic or virus populations. Dimensionless time n2=t/T2, where T2 there is average time of an individual life of the second population. For example, for a virus of flu is T2≈ 7 days 3, 4, 5. The mutagen factor working on immune system of the first population on second, is designated D1,2.
Let's enter uniform dimensionless time. From a condition n1T1 = n2T2 we find n2=(T1/T2)n1=(1/γ)n1
where a constant γ = T2/T1≈0,05 Hence the equation (2) can be copied as:
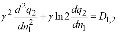 …..(3)
…..(3)
Let's examine the mutagen factors. We shall assume that allele in genome of the second population q2 at interaction with the first population it is inserted in a genome of the first population with catastrophic for a cell of the first population consequences. Hence, it is possible to assume that the mutagen factor is D2,1=α1q2 where α1<0 there is some constant factor.
Influence of the first population on the second consists in destruction by immune system of the first population of individuals (viruses) of the second population. Hence, it is possible to assume that D1,2 = α2, and size α2<0.
Thus the equations (1) and (3) get a kind:
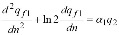 ...(4)
...(4)
 .....(5)
.....(5)
In the equations (4) and (5) index at dimensionless time is omitted since transition by uniform dimensionless time n=n1 was carried out.
Development of a Virus population During Time of Pandemic
The equation (5) for the second (virus) population at influence on it of the first population immune system can be solved irrelatively of the equations (4).
We integrate once the equation (5):
 .....(6)
.....(6)
Where C1 there is a constant of integration.
For the solution of the equation (6) we shall present function q2 as product of two functions q2=uv . Then the equation (6) will be copied as:
 …..(7)
…..(7)
Grouping the terms we shall find:
 ....(8)
....(8)
Expression in brackets we shall accept equal to zero γdu/dn+ln2u=0. Integrating this equality we shall find lnu=-ln2n/γ=-ln2n/γ . Hence there is u=2-n/γ. A constant of integration it is accepted equal to zero since there is some arbitrariness in a choice of function u. Substitute this function in (8) we shall receive:
 .....(9)
.....(9)
Solving the equation (9) concerning function V we find:
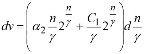 .....(10)
.....(10)
Hence:
 …..(11)
…..(11)
Thus for allele frequency q2 we shall find:
 ....(12)
....(12)
We use the following conditions: at n=0 the allele frequency is q2 = q20, at n/γ=1/ln2 allele frequency is 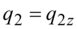 . The second condition is equivalent to time t=1.443t2, i.e. the second condition is accepted for time approximately in one and a half time more than average time of an individual life of the second population.
. The second condition is equivalent to time t=1.443t2, i.e. the second condition is accepted for time approximately in one and a half time more than average time of an individual life of the second population.
Hence on the first condition:
 ….(13)
….(13)
on the second condition:
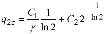 ….(14)
….(14)
Solving the system (13), (14) we find:
 …...(15)
…...(15)
 ….(16)
….(16)
Substituting (15) and (16) in (12) we shall receive:
 ……..(17)
……..(17)
The formula (17) can be written down as the sum of two terms: reflecting duplication in the second (virus) population and influence on it first population:
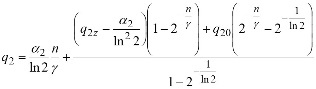 .....(18)
.....(18)
Let's note that duplication in a virus population occurs not independently but only at interaction to cells, for example, a human population. Therefore at the first term (18) there is a size γ=T2/T1 dependent on average time of a cell life of the first (human) population. The second term (18) reflects action of the person immune system on the second (virus) population.
On Figure 1 change of an allele frequency q2 the second (virus) population in time at absence of influence of the person immune system (curve 1), and at presence of influence (curve 2) of the first population immune system is shown.
Figure 1.Change of an allele frequency q2 in time for the second (virus) population at absence of influence of the first (human) population immune system, a curve 1 and at presence of influence, a curve 2. Parameters for calculation q0 =0,3;; q2=0,65; γ=0,05;α2 = -0.01.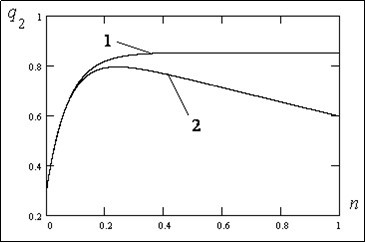
From the analysis of graphs it is visible that at absence of influence of a human population immune system on a virus population there is a gradual growth of the allele frequency q2 in time; the approach of allele frequency q2 to equilibrium value. At presence of influence of the first (human) population immune system the growth q2 is replaced by falling due to destruction of viruses at action of immune system of the first population.
Development of a Human Population During Time of Pandemic
The most interesting question it is work of organism cells of a human population at their interaction with viruses. Some results of such interaction can be received at the solution of the equation (4).
The solution of the equation (4) can be received substitution of the solution (18) in the equation (4). However such way is difficult occurrence of complex function in the right part of the equation (4). Therefore we shall increase the order of the equation having substituted function q2 from the equation (4) in the equation (5). In result we shall receive the linear differential equation of the fourth order:
 ....(19)
....(19)
Integrating the equation (19) twice we find:
 …(20)
…(20)
where C3 and C4 there are constants of integration.
For the solution of the equation (20) we shall find the general solution of the homogeneous equation. We shall write down the characteristic equation:
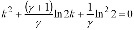 …..(21)
…..(21)
Solutions of a quadratic equation (21) look like:
K1 = -ln2, K2 = - ln2/γ ….(22)
Hence the general solution of the homogeneous equation looks like:
 …..(23)
…..(23)
Where C5 and C6 there are constants of integration.
The particular solution of the equation (20) we shall search as a polynom:
 …….(24)
…….(24)
where A, B and D there are constant factors.
Substituting (24) in (20) we shall find:
 .....(25)
.....(25)
Equating factors at identical degrees n we find:
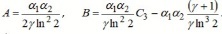 ......(26)
......(26)
ConstantD in (24) to find there is no necessity.
Thus the particular solution (24) of equation (20) looks like:
 ….(27)
….(27)
Hence the solution of the equation (20) will be written down as the sum (23) and (27):
 ......(28)
......(28)
Let's accept the initial condition: at n=0 size is qf1 = qf0.
Hence:
qf0 = C5 + C6 + D …….(29)
Thus:
 .....(30)
.....(30)
The found solution (30) characterizes the sum of two processes: duplication of individuals of the first population - first three terms, and the influence on a population - the fourth term.
Absence of influence on the first population there are probably in two cases. First, at α1 = 0 , i.e. the second population does not operate on the first population; second, at α2 = α1 = 0 these populations develop independently from each other and thirdly, zero value of expression in brackets of the fourth term (30).
Last case is most interesting. It is connected to a variant when on the first population, for example, human, was influence of the second population, for example, virus, but then it has stopped since the human population has developed immunity to influence of a virus population.
Let's equate last bracket (30) to zero:
 .....(31)
.....(31)
The equation (31) allows find dimensionless time of immunity development at the first population to influence of the second population:
 …..(32)
…..(32)
Dimensional time is equal:
 .....(33)
.....(33)
Unfortunately, the formula (33) has a uncertain constant C3.
The constant C3. is defined according to (19) the sum of initial values of first three derivatives on time from the allele frequency qf1. Integrating (19) once at n=0 we shall find:
 ……..(34)
……..(34)
Let's assume γ = T2/T1 very small size. It is possible since average time of a cell life of the person usually is much greater average time of a virus life. In this case according to (34) a constant is C3 ≈0.
The formula (30) at C3 ≈0 also γ<<1 looks like:
 .....(35)
.....(35)
At C3 ≈0 dimensionless time of influence attenuation of the second population on the first population (32) it is equal , nlmm =2/ln2 ≈ 2,9 dimensional time (33) is equal tlmm =2/ln2 ≈ 2,9T1≈400days. Found time of collective immunity occurrence - almost 3 average of time of a cell life of an individual. After the ending of influence of the second population on the first the last term in (35) becomes equal to zero. There is a free duplication in the first population. Taking into account also γ<<1 it is possible to write down:
 .....(36)
.....(36)
The law of free duplication of a population looks like 1, 2:
 …..(37)
…..(37)
where qfo there is initial frequency of examined recessive allele at the woman, qm0 - at the man.
Comparing (36) and (37) we find C5 = (qf0 - qm0)/3. As it was supposed, appeared C6 = 0, since qf1 at free duplication of individuals should not depend on size γ. Therefore the formula (35) can be copied as:
 …... (38)
…... (38)
On Figure 2 change of an allele frequency qf1 the first (human) population in time at absence of influence (curve 1), and at presence of influence (curve 2) of the second (virus) population is shown.
Figure 2.Change of the allele frequency qf1 in time at the first (human) population at absence of influence of the second (virus) population (curve 1) and at presence of influence (curve 2). Parameters for calculation qf0 = 0,3; qmo = 0,3; γ = 0,005; α1 = -0.1; α2 =-0.01.
From Figure 2 it is visible that allele frequency at absence of influence of a virus population gradually falls coming nearer to equilibrium value qf1 = (2qf0 + qmo)/3 = 0,23 . At influence of a virus population the allele frequency on which influence is carried out (curve 2) first falls very quickly due to destruction of cells and accordingly alleles but then in process of development of immunity at nimm = 2/ln2 ≈ 2,9 and duplication of cells the frequency grows reaching the normal level corresponding to a curve 1. The further growth of a curve 2 shown by a dotted line apparently of biological sense has no.
Conclusion
The used genetic-mathematical model of interaction of the populations based on the Hardy - Weinberg law allows calculate some distinctive features of process of interaction of populations. It can be used at an estimation of duration of pandemic COVID-19.
It is marked that the virus population actions not with a human population as set of very complex organisms, and with a population of separate cells of the person bodies. As an example cells of a liver are used. It is shown that duration of pandemic process in this case makes approximately 400 day.
With the help of the equations of a population development it is shown that cells of a human population first intensively perish under influence of viruses but then at development of the immune answer due to duplication of cells the organ of the person is restored up to a normal level. The destruction of an individual (person) at virus attack is exclusive enough event connected to full destruction already beforehand weakened organ for accompanying reasons.
Dynamics of development of a virus population at its interaction with a human population is shown. Intensity of destruction of viruses in particular a flu as well investigated disease at action of immune system of the person is designed.
