Abstract
In the last decade, the amount of collected data, in various computer science applications, has grown considerably. These large volumes of data need to be analysed in order to extract useful hidden knowledge. This work focuses on association rule extraction. This technique is one of the most popular in data mining. Nevertheless, the number of extracted association rules is often very high, and many of them are redundant. In this paper, we propose an algorithm, for mining closed itemsets, with the construction of an it-tree. This algorithm is compared with the DCI (direct counting & intersect) algorithm based on min support and computing time. CHARM is not memery-efficient. It needs to store all closed itemsets in the memory. The lower min-sup is, the more frequent closed itemsets there are so that the amounts of memory used by CHARM are increasing.
Author Contributions
Academic Editor: Erfan Babaee, Mazandaran University of Science and Technology, Iran.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2020 Youssef Fakir, et al.
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
The field of data mining appeared with the promise of providing the tools and techniques to discover useful and previously unknown knowledge in these data fields. Data mining has been adopted for researches dealing with the automatic discovery of implicit information or knowledge within the databases 1. The implicit information contained in databases, principally the interesting association relationships among sets of objects may reveal useful patterns for decision support, marketing policies, financial forecast, even medical diagnosis and many other applications 2. Figure 1 illustrate a flow chart of datamining techniques.
Figure 1.Datamining techniques
The issue of mining frequent itemsets emerges first as a sub problem of mining association rules. Frequent itemsets play a vital role in many data mining tasks that try to find compelling patterns from databases such as association rules, classifiers, correlations, clusters, sequences, and many more of which the mining of association rules is one of the most famous problems 3, 4, 5. Mining frequent itemsets or patterns is a fundamental and indispensable problem in numerous data mining applications.
The original reason for searching association rules came from the need to analyse supermarket transaction data, that is, to examine client’s behaviour in terms of the purchased products. Association rules describe how often items are bought together. For example, an association rule: {milk-oil (76%)} assert that 6 out of 7 clients that bought milk also bought oil. Such rules can be practical for decisions about product pricing, promotions, store arrangement and many others.
The extraction of association rules is primarily based on two fundamental notions: support and confidence.
To determine these rules, support and confidence need be at least equal to minimum thresholds of minimum confidence and minimum support described via the user. For this, the search for association rules has been oriented towards these two objectives:
a. Determine the set of frequent itemsets that appear in the database with support greater than or identical to minsup. The problem of the extraction of frequent itemsets is of exponential complexity in the size m of the set of items as the number of potential frequent itemsets is 2m. Then, the phase of searching for these items and frequent is the costliest extraction of association rules.
b. Generate the set of associative rules, from these frequent itemsets, with a confidence measure greater than or identical to minconf. Indeed, the time of this phase is very small compared to the cost of extracting frequent itemsets because the generation of association rules is a problem that depends exponentially on the size of set in a frequent itemsets. Once all frequent itemsets and their support are known, the association rule generation is straightforward. Hence, the problem of mining association rules is reduced to the problem of determining frequent itemsets and their support.
In this paper, we show that it is not requisite to mine all frequent itemsets to guarantee that all non-redundant association rules will be found. Therefor we are going to discuss two approaches:
a. Approach based on the discovery of "closed" itemsets, coming from the theory of formal concepts propose to generate only a compact and generic subset of associative rules. This subset is much smaller than the size of the set of all rules. We show that it is sufficient to consider only the closed frequent itemsets. Moreover, all non-redundant rules are found by only considering rules among the closed frequent itemsets. The set of closed frequent itemsets is much smaller than the set of all frequent itemsets. This approach proposes to reduce the cost of extracting frequent itemsets based on the fact that the set of frequent closed itemsets is a generating set of the set of frequent itemsets. This approach makes it possible to decrease the number of extracted rules by keeping only the interesting ones to give the possibility to better visualize them and exploit them.
b. Approach that uses maximal frequent itemsets: A maximal set of elements is a frequent set of elements that is not included in an appropriate superset that is a common set of elements. The set of frequent maximal items is therefore a subset of the set of frequent closed items, which is a subset of frequent itemsets. That makes the set of frequent maximum items usually a lot smaller than the set of frequent items and smaller than the set of frequent closed items.
This paper also gives the comparison of algorithms based on execution time and support value. The paper is organized as follows. Section 2 deals with the association Rule Mining Algorithms (CHARM algorithm). Section 3 present the experimental results. Conclusion is given in section 4.
Charm Algorithm
After developing the main ideas behind closed association rule mining, we now present CHARM 5, an efficient algorithm for mining all the closed frequent itemsets. First, we will describe the algorithm in general terms, independent of the implementation details. Later we will show how the algorithm can be implemented successfully.
Developed by Zaki and al 6 CHARM Algorithm is an efficient algorithm for enumerating all closed elements. A number of innovative ideas are being used in the development of CHARM, which have made it the choice forever for the extraction of frequent closed itemsets among the benefits of CHARM:
CHARM simultaneously explores the item space and the transaction space, above a new IT-tree 7 search space (tree of itemsets-tidset). On the other hand, most methods use only the item search space.
CHARM uses a highly efficient hybrid search method that ignores multiple levels of the computer tree to quickly identify frequent closed-element sets, instead of having to enumerate many possible subsets.
It uses a hash-based fast approach to remove non-closed items when checking for under-consumption.
CHARM also uses a new vertical representation of data called diffset 8, 9, for fast frequency calculations. Diffsets keep track of differences in the details of a candidate pattern from its prefix pattern. The diffsets significantly reduce (in order of magnitude) the memory size needed to store the intermediate data.
The CHARM Algorithm Goes Through 3 Phases
Enumeration of closed sets using a double tree of itemset-tidset (itemset -transaction identification set) search.
Using the technique called diffsets to reduce the memory footprint of intermediate calculations.
Finally, uses a hash-based fast approach to remove all "unclosed" sets found during the calculation.
The pseudo algorithm of CHARM is shown in Figure 2.
CHARM begins by initializing the class of prefixes P of the nodes to be examined by the frequent 1-itemsets and their associated tidsets (transaction identification set). The two generic steps are instantiated as follows:
Pruning Step
This step is implemented via the CHARM-PROPERTY procedure (Figure 4). This procedure can modify the current class P by deleting IT-pairs or by inserting new ones in Pi. An IT pair is first pruned compared to minsup. Then, we check if it is maximum or not. To do this, just check that its Tidset is included in that of the pair that generated it. Once all the IT-pairs have been processed, the new class Pi is recursively explored in depth first, by calling the CHARM-EXTEND procedure (Figure 3).
Construction Step
This stage is implemented via the CHARM-EXTEND procedure. It combines the IT-pairs, which appear in the class of prefixes P. For each IT pair Xi × (Xi)J, it combines it with other IT pairs Xj × (Xj)J following it in lexicographic order. Each Xi will generate a new class of prefixes Pi, which would initially be empty. The two IT-pairs combined will produce a new pair X × Y, where X = Xi ∪Xj and Y= (Xi) ∩ J (Xj)J.
Finally, the algorithm gives in its output FC (The Set of Frequent Closed Itemsets) that we seek.
The algorithm is programmed on Java. We illustrate the CHARM algorithm on the following example that describes purchased products in an electronics store (Table 1 and Table 2) by choosing a minisupport =3.
Table 1. Item sets| Scanner | PC | Notebook | Laser | Printer |
| A | C | D | T | W |
| Transaction Id | Purchased items |
| 1 | A C T W |
| 2 | C D W |
| 3 | ACTW |
| 4 | ACDW |
| 5 | A C D T W |
| 6 | C D T |
In Table 2 we describe the database in horizontal format, each record is a required set. A separate number named transaction ID is assigned to each record. Table 3 show the database in vertical format, where each record is a transaction identifier set relating to an article. This item appears in these transactions. This format will help us during the process of making the IT-tree (itemset-tidset tree). Table 4 represent the items and their apparition in transaction of Table 1.
Table 3. Vertical format database (left), Binary representation (right)| A | C | D | T | W | TID | A | C | D | T | W |
| 1 | 1 | 2 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |
| 3 | 2 | 4 | 3 | 2 | 2 | 1 | 1 | 1 | ||
| 4 | 3 | 5 | 5 | 3 | 3 | 1 | 1 | 1 | 1 | |
| 5 | 4 | 6 | 6 | 4 | 4 | 1 | 1 | 1 | 1 | |
| 5 | 5 | 5 | 1 | 1 | 1 | 1 | 1 | |||
| 6 | 6 | 1 | 1 | 1 |
| Purchased items | Apparition in | count | Purchased items | Apparition in | Count |
| A | 1345 | 4 | DW | 245 | 3 |
| C | 123456 | 6 | TW | 135 | 3 |
| D | 2456 | 4 | ACD | 45 | 2 |
| T | 1356 | 4 | ACT | 135 | 3 |
| W | 12345 | 5 | ACW | 1345 | 4 |
| AC | 1345 | 4 | CDT | 56 | 2 |
| AD | 45 | 2 | CDW | 245 | 3 |
| AT | 135 | 3 | CTW | 135 | 3 |
| AW | 1345 | 4 | DTW | 5 | 1 |
| CD | 2456 | 4 | ACDT | 5 | 1 |
| CT | 1356 | 4 | ACDW | 45 | 2 |
| CW | 12345 | 5 | CDTW | 5 | 1 |
| DT | 56 | 2 | ACDTW | 5 | 1 |
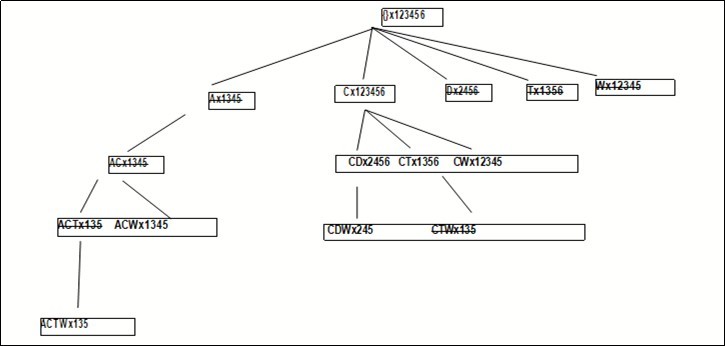
Let Itemset X, t (X) be the set of all tidset that contains X. CHARM searches for frequent closed sets on a new search space in the IT-tree where each node is a pair X × t (X), for example: AT × 135. All children in node X share the same X prefix and belong to the same equivalence classes. According to these, we can set our It-tree as illustrated in Figure 5 by using Table 4.
Initially we have five branches, corresponding to the five items and their tidset from our example database. To generate the children of item A (or the pair A 1345) we need to combine it with all siblings that come after it. When we combine two pairs X1 t(X1) and X2 t(X2), we need to perform the intersection of corresponding tidset whenever we combine two or more itemsets that is how we got the It-tree above. After sitting our new search space now, we proceed with the charm algorithm steps.
When we try to extend A with C, we find that t(A)=1345⊂ t(C)=123456. According to CHARM-PROPERTY we can thus remove A and replace it with AC combining A with D produces an infrequent set ACD, which is pruned. Combination with T produces the pair ACT135. When we try to combine A with W, we find that t(A) ⊂t(W), we replace all unpruned occurrences of A with AW. Thus, AC becomes ACW and ACT becomes ACT W. At this point there is nothing further to be processed from the Abranch of the root.
We now start processing the C branch. When we combine C with D, we observe that t(C) ⊃ t(D). This means that wherever D occurs C always occurs. Thus, D can be removed from further consideration, and the entire D branch is pruned, the child CD replaces D. Exactly the same scenario occurs with T and W. Both the branches are pruned and are replaced by CT and CW as children of C. Continuing in a depth-first manner; we next process the node CD. Combining it with CT produces an infrequent itemset CDT, which is pruned. Combination with CW produces CDW. Similarly, the combination of CT and CW produces CT W. At this point all branches have been processed.
Finally, we remove CTW 135 since it is contained in ACT W 135. As we can see, in just 10 steps we have identified all 7 closed frequent itemsets. The routine CHARM-PROPERTY simply tests if a new pair is frequent, discarding it if it is not. It then tests each of the four basic properties of itemset-tidset pairs, extending existing itemsets, removing some subsumed branches from the current set of nodes, or inserting new pairs in the node set for the next (depth-first) step. At the end, we get our new It-tree whom now holds only closed frequent itemsets as illustrated in Figure 6.
Result and Discussion
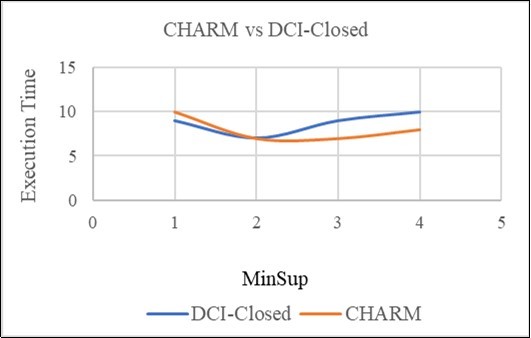
The Algorithms was coded in Java using the dataset collected from electronics stors. For the comparison we used DCI-closed, a famous algorithm for mining frequent closed itemsets to be compared with CHARM Algorithm. For performance comparison, we used the original source or object code for DCI-closed provided to us by 10. Figure 7 illustrate the execution time in the data of both algorithms with different minsup. Comparing with DCI-closed, we find that both CHARM and DCI-closed have similar performance for lower minimum support values. However, as we increase the minimum support, the performance gap between CHARM and DCI-closed widens. For example, at the highest support value plotted, CHARM is faster than DCI-closed in execution time, which makes CHARM, outperforms better on higher support than the DCI-closed for our database.
Conclusion
In this paper, an efficient algorithm (called CHARM) for mining closed frequent itemsets is presented. Using an new IT-Tree framework, this algorithm explores simultaneously the itemset space and tidset space The IT-Tree skips many level to identify quickly the closed frequent itemsets. According to the experiment CHARM perform better on higher minsup compared to the algorithm DCI-Closed for mining closed patterns. CHARM faces a memory-inefficient challenge since it needs to maintain all closet itemsets in the memory to check if an itemset is closed or not. For this reason, an improvement of CHARM is necessary. As future work were are going to optimise CHARM.in order to solve the memory-inefficient.
References
- 1.Agrawal R, Mannila H, Srikant R, Toivonen H, Inkeri A. (1996) Verkamo. Fast discovery of association rules. Advances in Knowledge Discovery and Data Mining In U. Fayyad and et al, editors , Menlo Park, CA 307-328.
- 2.M J Zaki. (2000) Scalable algorithms for association mining. , IEEE Transactions on Knowledge and Data Engineering 12(3), 372-390.
- 3.Zaki M J, Gouda K. (2001) Fast vertical mining using Diffsets,Computer Science Dept, Rensselaer Polytechnic Institute. Technical Report,1-1
- 4.Mohamed El far, Moumoun Lahcen, Gadi Taoufiq. (2010) An Efficient CHARM Algorithm for indexation 2D/3D and Selection of characteristic views. 5th International Symposium On I/V Communications and Mobile Network .
- 5.Burdick D, Calimlim M, Gehrke J. (2001) MAFIA: a maximal frequent itemset algorithm for transactional databases. In Intl. Conf. on Data Engineering .
- 6.Zaki M J, Hsiao C J. (1999) CHARM: An efficient algorithm for closed association rule mining.Computer Science Dept., Rensselaer Polytechnic Institute. Technical Report 99-10
- 7.Han J, Wang J, Lu Y, Tzvetkov P. (2002) Mining Top-k frequent closed patterns without minimum support. ICDM'02.
- 8.Liu J, Pan Y, Wang K, Han J. (2002) Mining frequent item sets by opportunistic projection. SIGKDD'02.
- 9.Pan Yi, Hong Yan Du. (2011) A Novel Prefix Graph Based Closed Frequent Itemsets. the 14th IIEE International Conference on Computational Science and Engineering .
- 10.Ye Xin, Wei Feng, Jiang Fan, Cheng Shaoyin. (2015) An Optimization to CHARM Algorithm for Mining Frequent Closed Itemsets. IEEE International Conference on Computer and Information Technology; Ubiquitous Computing and Communications; Dependable, Autonomic and Secure Computing; Pervasive Intelligence and Computing .