Genetic-Mathematical Modelling of Mutational Processes in a Population

Before to proceed to studying influence of the mutational factor to a population we shall consider some mathematical questions of genetic inheritance in case of this factor absence influence.

For a family tree the analysis we shall carry out on the basis of Hardy – Weinberg law ³. This law in the elementary kind of two alleles of a gene establishes that relative frequencies of genotypes in generations of a family tree correspond to members of binomial expansion (p + q)² so p + q = 1 where p and q frequencies of a dominant A and recessive a alleles in a family tree. It is supposed that a modeling family tree large enough so it is possible inbreeding to neglect. Besides there exists panmixia, is no selection, mutations, migrations of individuals, etc. ¹.

According to this law genotypesАА,Аа, andаа at autosomal inheritance have the following frequency ratio:

(AA)p²: (Aa)2pq: (aa)q² …...(1)

The Hardy - Weinberg equilibrium state is indifferent. On the autosomal inheritance it is obvious. Really, using distribution of genotypes (1) it is possible to receive, for example, the frequency of a recessive allele a in the following (n + 1) generation. For this purpose it is necessary for the previous generation n to do summation of the half of heterozygotes frequencyАа, and the homozygotes frequencyаа:

……...(2)

In the following (n + 1) generation there is same frequency of a recessive allele a as in the previous n generation received.

For the linked to a sex genome the analysis is necessary more complex.

Let's assume that alleles A and a are linked to the Х-chromosome. The frequency of a dominant allele A in the men is p_m and in the women p_f . For recessive allele a it is accordingly q_m and q_f.

At crossing in the first generation there is a ratio of genotypes in the women according to product (p_f + q_f) (p_m +q_m):

……(3)

Using the distribution of genotypes (3) it is possible to find a frequency of allele a in the women for the following (n + 1) generation:

…..(4)

In the deduction (4) the following obvious ratios p_mn = 1-q_mn, and p_fn = 1-q_fn are used.

Thus, the frequency of allele a in the women for the following generation is equal to a half-sum of the allele frequencies a in women and man of the previous generation between whom there was a reproductive contact. The formula (4) can be copied in the following kind:

........(5)

For convenience of the formula (5) further analysis we shall write down it with displacement on one generation back:

.........(6)

At absence of mutagen effect the frequency of allele a at men is equal to frequency of this allele at women of the previous generation q_m(n-1) = q_f(n-2). Using the given condition, from (6) we shall find:

.........(7)

The solution of the finite-differential equation (7) we search as q_{fn =} bⁿ where in this caseb is constant. Substituting this solution in the formula (7) we have:

……...(8)

Let's divide the equation (8) on b ^n-2:

b - 2b² + 1= 0 ……..(9)

We find two roots of the characteristic quadratic (9):

b₁=1, and b₂=1/2, …..(10)

Hence the general solution of the finite-differential equation (7) looks like:

q_fn= C₁ + C₂(-1/2)ⁿ …….(11)

The formula (11) has been found by a different way in ⁴.

Constants of integration c₁ also c₂ we shall find on the basis of the initial conditions: at n=0 , q _fn=q _f0, and at n = 1 according to (4) q_fn = q_f1 = q_mo + q_f0 / 2. Thus:

C₁ = 2q_f0 + q_m0 /3, and C₂ = q_f0 + q_m0 / 3. ….(12)

Therefore the solution (11) finally looks like:

.......(13)

On figure 2 the dependence of a recessive allele a frequency linked with the Х-chromosome in a family tree at the women from the number of generation n plotted under the formula (13) is shown.

The initial conditions for calculation are accepted q_f0 = 0.6, and q_m0 = 0.2. The figure 2 shows how a recessive allele a frequency at women during crossings comes nearer to the equilibrium frequency q_fn = 2q _f0 + q _m0 / 3 = 0.467.

Hardy - Weinberg law in the form before considered concerns to a separate family tree. Implicitly this law includes time because alternation of generations occurs through certain time. Thus Hardy - Weinberg law has the discrete character on time. The population will consist of family trees crossed among themselves and lives in continuous time. Alternation of generations of the family trees set results to generations are replaced actually according to a continuous time scale.

In it the basic distinction of the Hardy - Weinberg law for a population and a family tree. In earlier used form (1) Hardy - Weinberg law is written down for a family tree.

Let's pass to a continuous scale of the generations n. Under size n in this case we mean time t lives of the population normalized on average on a population time of a one generation life, i.e. actually continuous dimensionless time n = t/T.

Let's find out, whether there is the differential equation having the characteristic equation similar (8).

For this purpose we shall consider the differential equation:

…….(14)

where Ƞ is constant. In this formula q_f(n-1) there is recessive allele frequency at the woman in n - 1 generation. Differentiation in (14) goes on dimensionless time n.

Let's transform the equation (14) to finite-differential form:

…….(15)

where size Δn there is the time step of finite-differential representation of a derivative.

Uniting similar members and multiplying the equation (15) on - 2 we shall find:

......(16)

Let's try to identify the equations (16) and (7) for alternation of the recessive allele frequencies in generations of a family tree. For this purpose it is necessary to accept:

2(2 - ȠΔn) = 1, and -2(1 - ȠΔn) = 1 …….(17)

Wonderful feature of the algebraic equations (17) is that they have the identical solution:

ȠΔn = 3/2 …...(18)

It’s means that the finite-differential equation (7) and the differential equation (14) can have the same characteristic equation. Taking into account (18) the equation (14) can be copied as:

……..(19)

The equation (19) can be integrated once:

……..(20)

where C₁ is constant of integration.

Further integrating the equation (20) by method of a separation of variables:

…….(21)

Where q _fo there is initial frequency of examined recessive allele at the woman we shall find q^fn= q_f(n) - the time dependence of it allele on frequency:

……..(22)

Identifying the solution (22) with the solution (13) we shall find:

and

……..(23)

Where q_m0 there is initial frequency of examined recessive allele at the man.

As it was expected the formulas (23) do not contradict each other. Hence, the solution (22) can be written down as:

.........(24)

The formula (24) is correct for frequency of female allele a only in even generations. This is consequence of transition to the continuous scale of the time n.

Comparing (13) and (24) for even generations we have 2^-n=e-3/2Δn ⁿor Δn = 3/2ln 2 . Hence (24) it will be transformed to the kind:

…...(25)

that is identical to the formula (13) for even generations n. But in (25) as against (13) the size n is a dimensionless time. Numbers of generation in (25) are not present.

Taking into account (18), and Δn = 3/2ln 2 we shall find Ƞ=ln 2. Thus the differential equation (19) will be written down as:

........(26)

As generations in a population are replaced continuously in the formula (26) there is no necessity to specify number of generation. The formula (26) represents Hardy - Weinberg law for a population. We shall note that Hardy - Weinberg law in form (26) as well as (1) reflects indifferent balance of a genome since to it satisfies the solution q_f = const.

On figure 3 dependence plotted under the formula (25) of allele a frequency linked withthe Х-chromosome in a population at women from dimensionless time n is shown at the same initial conditions as dependence on figure 2. Equilibrium frequency of allele there is same as well as in case of discrete alternation of generations in a family tree.

Figure 2.Dependence of a recessive allele a frequency in a family tree at women from the number of generation n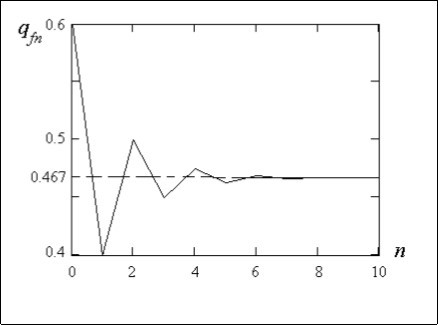

Figure 3.Dependence of a recessive allele a frequency in a population at women on dimensionless time n=t/T

Let's consider influence of some mutational factor on a population. It can be abrupt change of the environment characteristics: increase of ultra-violet or radioactive radiation, emission of harmful products of a natural (volcanic) or artificial origin, distribution of pesticides, etc. All these factors change of the alleles frequency in a population, i.e. cause genic modification.

It is possible to result as an example decrease in frequency of the recessive alleles of the genes determining the concentration of a catalase in blood in 15.5 times approximately for 2 generations for people living in Hiroshima and Nagasaki in comparison with other people of Japan. Herewith the frequency of the dominant alleles practically has not changed ⁵.

The characteristic of a system response on some influence generally is Green's function of this system ⁶. Therefore first of all we shall find Green's function for a population.

Let's consider the differential equation (26) reflecting the Hardy – Weinberg law for female allele linked with a sex for a population on which some mutational factor operates influencing only on a recessive allele a:

……..(27)

Where D (n) there is function of time describing influence of the mutational factor on a population.

Let's search the solution of the equation (27) as:

…….(28)

where q _f0 there is initial (before the beginning of influence on a population) frequency of recessive allele in the woman, G(n, n^| ) - Green's function for a population, n^| - the parameter of integration – time (moment) of mutational influence the response on which is investigated in time (moment) n, so n > n^/ .

Let's substitute the formula (28) in the equation (27):

...........(29)

Let's accept the following initial conditions reflecting that initial frequency of a recessive allele does not depend on time .

In this case the equation (29) will be transformed to a kind:

………...(30)

Where ẟ (n - n^/) there is Dirac’s function.

In (30) we used known property of Dirac’s ẟ - function ⁷:

……….(31)

where Dirac’s ẟ - function has the following determination ẟ (n - n^/) = 0 at n ≠ n^|, and ẟ (n - n^|) = ∞ at n = n^/.

Thus from the equation (30) we find the equation for Green's function of a population:

.........(32)

The linear differential equation of the second order (32) easily is solved by introduction of a new variable.

Let's note that Green's function of a population does not depend on a kind of influence. Green's function of a population is a characteristic of a population but of not the influence kind on it. It shows how the population reacts to conditional instant mutational influence as ẟ -function in the initial moment of time n - n^| .

Further assuming Z=uv we find the function v=e-^{n ln 2}. For function u the differential equation looks like:

......(33)

which solution is:

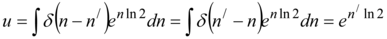
......(34)

In a finding (34) we are used the evenness of the ẟ-function and property (31). Hence there is. Z=uv=e^{-(n-n| )ln2}. Green's function of a population find by a condition:

.....(35)

Formula (35) can be presented as:

…….(36)

where Δn = n-n^| there is time interval from the moment of influence n^| .

The sign a minus specifies that the population always resists to the external influence.

On figure 4 the change of Green’s function of a population in case of the elementary two-allele system linked to a sex is shown. The minimal value of the Green’s function at Δn = 0 it is equal G(Δn) =-1.443. On Δn→ ∞ the Green's function is to tend to zero. Thus the response of a population to mutational influence it is gradual disappearance of an influence result. Actually, already in 4 - 5 generation a genome of a population comes back to an initial level which existed before the influence. Due to crossing the mutations as are soluble in a population. This fact is well-known to selectors. The cultural plants are given themselves quickly become natural.

Figure 4.Green’s function for the two-allele genomic system linked to a sex

Let's substitute Green's function (36) in the formula (28):

………..(37)

where

there is parameter of a mutation, and integration is carried out on all dimensionless time of the mutational factor influence from 0 up to n^|_max. We shall notice that as against the equation for Green's function (32) in the formula (37) time of influence not instant.

Thus the law (37) of a recessive allele frequency change at women in a population in response to mutational influence carries universal on time n character. Depending on a kind of mutational process changes only the parameter of a mutation M dependent also from duration of mutational process n^|_max.

For example if mutational influence is carried out with the help of gradually radioactive element decay, D(n^|)=D(0)2^-αn|8, where α=T/T_1/2 , and T_1/2 there is half-life of a radioactive element. Hence the parameter of a mutation is equal:

….(38)

The elementary formula for parameter of a mutation occurred if the half-life of a radioactive element is equal to average time of generation alternation, i.e. α=1. In this case the parameter of a mutation linearly depends on time of mutational influence M=D(0)n^|_max. For example to this condition for the person satisfy half-life of such widespread radioactive elements, as caesium Cs¹³⁷₅₅ - 30.2 years, strontium Sr⁹⁰₃₈ - 28.7 years ⁹ though it is usual half-life of radioactive elements much less.

If the radioactive doze is proportional to time of influence the linear dependence of parameter of a mutation on time of influence well correlates with the experimental linear curve “doze – effect” for Drosophila melanogaster³. Biophysical mechanisms of mutations at a radioactive irradiation are considered in ¹⁰.