Abstract
Four rules for good anatomical modeling of plants are explored. First, the cell is the reference source for modelling at any level. Second, developmental signaling occurs between few cells, about 12. Third, rules of are algorithmic and not simply physical forces as proposed by Thompson. Finally, it is desirable to proposed a likely alternative model that can be discounted. The main value of modelling is selecting data for modelling rather than the by a biased investigator.
Author Contributions
Academic Editor: Cumali Keskin, Artuklu University, School of Health, Turkey
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2018 Robert W. Korn
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
With the availability of the modern computer, complex modelling of many problems including biological development becomes accessible 1, 2, 3. The wide variety of problems requires an equally broad range of applications yet as a somewhat new methodology no ground rules have developed for modelling, each problem with its basic assumptions led to a somewhat specialized approach. For example, phyllotaxy (leaf arrangement) has been modelled along the lines of available space 4, pressure contact 5 diffusion of morphogens6. and they require special applications about geometry, force, and diffusion, respectively.
Modelling of plant anatomy comes in a variety of contexts. Three types of models used in biological development are (1) conceptual or the meaning of words such as sequence, origin, differentiation, etc.; (2) in vivo and in vitro or using living models and (3) in silica where models are paper-and-pencil or computer expressions 7. These three approaches are progressively more detailed as employed by the development of vascular bundles in monocots 8.
Results
All Changes are at the Cellular Level.
Of all the levels of organization in plant structure that of the cell stands since the formulation of the cell theory as the unit of function and reproduction 9. Structurally the plant cell is composed of facets that are arranged as an enclosure making function and multiplication possible. The cell then should also be the unit of modelling by which all other levels are possible. From a hierarchical point of view there are levels below and above that of the cell but are generated within the cellular enclosure and are active at different levels (Figure 1). Consider the levels of cell, tissue, organ and individual organism exemplified by a simplified plant leaf. One tissue is the epidermis which is seen as a composite of cell features, i.e, facets, vertices and contents and tissue features such as the middle lamella that holds cells together or a layer of cutin spread over the exposed facets. The contents of these features are made in cells and transported to specific facets. The case for organs is the same. What holds the epidermis and mesophyll together is also the middle lamella but only weaker as pieces of the epidermis can be peeled off without disassociating cells of the epidermis. And again, the component molecules of the middle lamella are synthesized in the enclosed protoplast and transported elsewhere and at different levels. The highest anatomical level is the organism which is realized by middle lamella holding two or more organs together. Actually there are not just one or two features at a level but possibly many. For example, epidermal tissue has more than just specific composition of middle lamella and a waxy coat on the outside of cells as tissue features but also anticlinal cell divisions (no periclinal divisions) and growth in only two of three dimensions, as well as production of stomata and hairs, etc. As seen in Figure 1 features at various levels are expressed as cell features. The overall distribution of specialized walls at different levels appears more as a conglomerate then the classical pyramidal hierarchy.
Figure 1.Hierarchical diagramization of an multicellular plant (individual). Middle lamella (mitotic cell plate) at major anatomical levels include cell as black, tissue as yellow with gray shading, organ as purple and individual as red. Stem edge on right.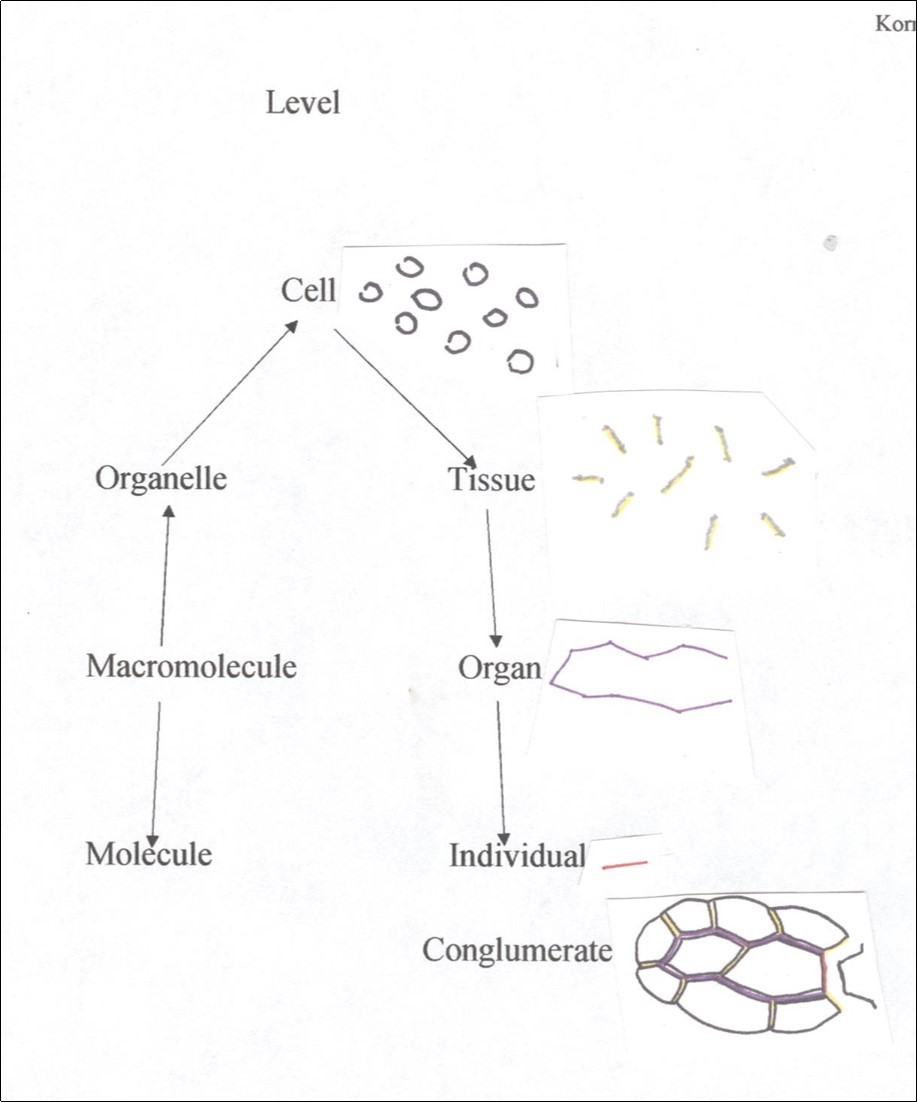
Small Size of Signaling
A common misconception is that since patterns are multicellular forming over large distances involving many cells when, in fact, only a few cells, about 12 or fewer, are involved at any one time in a cell-cell interaction. The pattern of parallel watermelon stripes is one such case. The earliest stage with a complete complement of stripes is in a fruit only 5.0 mm long with a surface area of 10.47 mm210 and the last stage has a SA of 33,000 mm2 for a 3,152-fold increase in size..
Veins also seem to form in small patches of cells. Branching of minor veins in leaves of Coleus and Similax occur in small groups of about 12 cells or less which later proliferate and enlarge 11. Contrary, rare cases of patternization in full-sized adult tissue is vein regeneration 12.
Groups, or modules, often overlap making development complicated. For example, a stomatal initial cell is surrounded by an average of six inhibited cells for a module of seven cells. But an inhibited cell is shared by two or three adjacent stomata and so modules overlap.
Additions are Algorithmic
A developmental model attempts to explain the origin of architectural order in sequential fashion. Each step in the model is a result of signaling originating at the cellular level. The first step is gratuitously given by the investigator and placed in the program and all later ones are derived from states generated during earlier steps. For example, the vascular bundle in the corn stem seems to come from only one bipolar cell from which all other cells are derived 8. On the other hand, the diffusion-reaction system 13 begins with a field of cells, two morphogens having particular diffusion and synthesis constants as givens. But later the investigator increases the concentration of one of the morphogens in one cell significantly greater than that expected by chance, ab externa, an unacceptable operation for modelling but acceptable in drawing. This can be symbolized as
in which cell X in state a changes to state b in the presence of agent Y in state c. Agent Y can be either derived from some part of the model or what an investigator gratuitously adds. A drawing is total gratuity. The fewer the gratuities the better the model.
Hellwig et al. made epidermal cells from an array of semi-organized loci and converted them into polygons by Voroni triangulation 5. The history of a cell is not a locus. Also, Jönsson et al. 6 modelled phyllotaxy patterning using a field of cells originally spherical with random arrangement of daughter cells The history of a cell is not that it once was bubble-shaped. Finally, available space explains where a new leaf forms 4. In these three cases of high morphogen concentration cells from loci and arrangement of daughter cells have no cellular origin, that is, have no history. By contrast, an algorithm for cell shapes and sizes was constructed using two rules 4. One, a new cell plate passes through the cell center, attaches perpendicular to the closest wall sites d distance from existing vertices to give somewhat similar cell sizes and only 3-rayed vertices. And rule two, the cell plate does not expand for one cell generation to shift angle sizes in vertices from 90o and 180o closer to 120o, changes using existing morphologies. These two algorithms apply to both 2D and 3D configurations of undifferentiated cells .Alteration of these two algorithms can produce a wide variety of differentiated cell types. Generally legitimate models are a composite of mostly non-gratuitous algorithms where cells have a history.
An investigator’s gratuitious addition is acceptable if a change can be generated by first an ‘in house’ algorithm and then is replaced by a generic change. For example, molecular diffusion creates a pattern that can be replaced by an equation at the tissue level or higher. This replacement has two advantages. First, it is a simplification requiring less computer space and therefore less running time and, second, the replacement is more generic and therefore allows modelling to operate at a higher hierarchical level, namely, from molecules to facets to cells to tissue to organs to the organism. The disadvantage is in rare cases problems encountered at extreme ends of distributions that can lead to meaningless states such as a cell smaller than its nucleus.
Alternative Explanations
Feller 15 noted that the logistic equation used to explain growth data is only one of several equations (Cauchy and normal distributions among others) that fit the data and sometimes even better than the logistic equation. This situation also fits processes other than growth as potentially having alterative explanation(s) (not to be confused with an alternative hypothesis to the null hypothesis). Usually a model is proposed without considering alternatives much less discounting them. Schwabe 16 counted 32 explanations for the phyllotaxy pattern, a number that has since increase at least by five.
An interesting situation is the shape of epidermal and parenchyma cells. Thompson 17 explained these shapes by simple physical force while as shown above can also be explained by two simple algorithms 8.
Major ideas in science do not seem to be based on strong evidence but by simply discarding less interesting ideas. The atomic theory, the cell theory and natural selection became more popular and exciting than Machian fluid theory of matter, colloidal theory of life and inheritance of acquired characteristics. As long as an idea does not contradict available facts, namely, is equivocal in supporting more than one explanation, an idea survives. The difficulty in attempting to eliminate an explanation first finding a criterion applicable to both explanations.
Conclusions
Modelling as presented in this study serves two purposes. First, it provides a more objective means of selecting the most fundamental features for describing ontogeny. Historically, investigators were biased in determining which features are the most interesting from a developmental view without considering their fate. With modelling, selection of traits has four guidelines: traits arise at the cell level, patternization occurs within a few cells, making of traits is algorithmic and not physical while description uses the best available explanation leading to discarding other hypotheses.
Second, modelling attempts to explain the origin of cell types as well as the number of each type. Again, these four guidelines apply for signaling between cells that includes monitoring of cell generations.
References
- 1.Prusinkiewicz P. (2004) Modelling plant growth and development. , Current Opinion in Plant Biology 10, 79-83.
- 4.Prusinkiewicz P, Runions A. (2012) Computational models of plant development and form.New. Phytologist193: 549–569,doi: 10.1111/j.1469-8137.2011.04009.xHofmeister,W.(1868)Allgemeine Morphologie der Gewachse. HandbuchderPhysiologischenBotanik , Leipzig, Engelmann 1, 405-664.
- 5.Hellwig H, Englemann R, Deussen O. (2005) Contact pressure models for spiral phyllotaxis and their computer simulationJ.Theor. , Biology240: 489 – 500, 10-1016.
- 6.Jonsson H, Heisler M G Shapiro, E B, E M Meyerowitz, Miolsness E. (2005) an auxin-driven polarized transport model for phyllotaxis. , PNAS 103, 1633-1638.
- 8.Korn R. (2016) Modelling the vasculature of the stem ofCyperusinvolucrausRottb.: evidence for three patterns of vascular bundles. , Planta 244, 103-110.
- 9.DeVos D, Dzhurakhalov A, Draelants D, Bogaerts I, Kalve S et al.Towards a mechanistic models of plant organ growth. , Journal of Experimental Botany 63, 325-3337.
- 10.Korn R. (2007) Watermelon stripes. A case for the clonal mosaic model in Plants. , J. Theor. Biol 10, 859-861.
- 11.Korn R. (2006) Tracheid analysis and modeling of the minor veins of the Coleus and Smilax leaves. , Planta 224, 915-923.
- 13.Segel.. L.A.(1980) Mathematical Models in Molecular and Cellular Biology.CambridgeUniversityPress 472.
- 15.Feller W. (1940) On the logistic law of growth and its empirical verification in biology. , Acta Biotheoretica 5, 51-66.

