Abstract
Objectives
Aim of the study was to develop a ‘composite body size score’ (CBSS) using anthropometric traits to estimate body size and to assess the nutritional status of each study individual on the basis of CBSS.
Materials and Methods
Data on seventeen anthropometric traits were collected from 710 individuals (Male, Female) from fishermen community inhabiting coastal villages of West Bengal, India. For estimating body sizes, Structural Equation Model (SEM) was constructed with Path Analysis (PA). Later, second order Confirmatory Factor Analysis (CFA) was applied on SEM to determine CBSS. It was hypothesized in the models that CBSS is composed with three sets of latent variables viz., linear, circular and skinfold, constructed from anthropometric traits. Applying new derived optimal cut off points of CBSS was used to determine lean, normal and robust body sizes. Individuals with negative values of CBSS were categorised as lean body size,. Positive values of CBSS were categorised into two categories- normal and robust body size.
Results
On the basis of CBSS, result showed that 50.6%, 48.8% and 0.6% of the individuals were categorised under lean, normal and robust body size respectively. Females showed relatively higher percent of lean body size i.e. under nutrition (73.8%) compared to males (26.2%).
Conclusion
The hypothesized model estimate more accurate composite body size score, based on anthropometric traits. All the traits are highly significant on the model. The lean body size category can be use in predicting ‘Undernutrition’.
Author Contributions
Academic Editor: Manal ElSawaf, anta University, al-Gaish Street, Tanta, Gharbia, Egypt.
Checked for plagiarism: Yes
Review by: Single-blind
Copyright © 2020 Baidyanath Pal
 This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
This is an open-access article distributed under the terms of the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Competing interests
The authors have declared that no competing interests exist.
Citation:
Introduction
The assessment of body size in adult populations has been established by several methods using different parameters 1, 2, 3. For example, somatotype of an individual, which provides information of body shape and size, is derived from selected anthropometric traits. The use of methods like, body mass index (BMI), waist hip ratio (WHR), fat mass index (FMI) and conicity index (CI), derived from anthropometric variables are mainly used to assess the nutritional status of a population. However, these techniques are perhaps neither comprehensive to assess the body size nor an appropriate measure of assessing nutritional status of individuals 4, 5, 6. Another study demonstrated using three techniques namely, mid upper arm circumference (MUAC), BMI (construct only two variables) and confirmatory factor analysis (CFA) (construct with more than two variables) in assessing the under nutrition and found that the statistical model, namely, CFA as the best measure compared to the other two 7, 8.
The use of statistical modelling in determining the best model fit of the data, association and distribution pattern among the parameters has come to use during the end of the 20th century 9, 10, 11, 12, 13, 14 highlighted statistical model for predicting the human head shape and 15 developed a statistical model for estimating the relationship between different anthropometric measures and standing height.
In India, attempts were made towards statistical modelling, concerned with the human body. For example, 16, 17 proposed a measure of group divergence and generalized distance (D2); 18, 19, 20 developed theories of statistics using anthropometric traits; 21 used univariate statistical analysis to describe the body composition and distribution of body fat between high and low altitude people of Himalayas. Moreover, 22 showed the relationship among the anthropometric variables at various high altitude populations. Besides these studies, a number of researchers 23, 24, 25 found the association of anthropometric traits with various parameters of biological and demographic aspects. However, none of the aforementioned studies attempted to provide an accurate statistical model to estimate different types of body size among individuals using anthropometric traits. Thus, it becomes imperative to develop a relatively improved model to capture the maximum variance among the parameters so that the model can be applied to every individual in a community or a population. Such a model needs to be developed with two important purposes (1) models should help in interpreting observed data using the measurement variables in the fitted model to the data and (2) models should be proposed to study the interaction of underlying variables (latent variables) in the future events.
To the best of my knowledge, in the Indian subcontinent, there is hardly any research which used anthropometric traits in developing a composite body size score to determine the body size.
In view of the above, the aim of the present study was to develop a composite size score using anthropometric traits to estimate body sizes and to assess the contribution of each of these anthropometric traits in determining body size.
Subjects and Methods
The study was conducted on a group of adult individuals belonging to a fishermen community inhabiting the coastal villages of East Midnapore district, West Bengal, India.
Anthropometric data were collected as a part of an intramural research project approved by the Technical Advisory Committee of Biological Science Division, Indian Statistical Institute, Kolkata in India entitled “Health and Disease among Population Inhabiting Contrasting Ecological Niches”. It was not feasible to conduct a sampling technique for selecting a random sample due to the lapse of the effects of the major biological factors regarding pedigree on inheritance. Purposive or representative sampling technique was used in order to involve maximum participants in the study. The bias of the data was previously estimated and was found negligible by 26.
Data Collection
This cross-sectional data were collected from 710 participants (Male, Female), aged 19-77 years. Two well-trained field investigators (one male and one female investigator measured respective gender groups) were employed to avoid measurement error. Each investigator was accompanied by a single recorder. Three consecutive readings were taken for each anthropometric measurement and finally, the average value within two decimal units was recorded.
Data Types
Seventeen anthropometric measurements were taken from each study participant following standard procedure 27. The following table lists the measurements, their abbreviated form (to be used in other sections subsequently) and the instruments used for measurements.
Statistical Background
In order to provide an effective and an appropriate statistical model, i.e., Structural Equation Model (SEM), a multivariate statistical technique was used for analyzing a hypothesized model. This technique can be described as a combination of both Path analysis and Confirmatory Factor Analysis (CFA), based on matrix algebra. All statistical analyses are described in the respective subsections.
Structural Equation Modelling (SEM): It is a comprehensive statistical approach to test hypotheses about relations among observed and latent variables 28. For SEM, there are two forms: (1) exogenous, that are always analogous to independent variables and (2) endogenous, which at some point act as dependent variables in the model while at other points may be independent variables. SEM was used to examine a series of dependence relationships between exogenous and endogenous variables simultaneously. 29 proposed the SEM as a methodology for representing, estimating, and testing linear relations between variables. 30 also said that it tests hypothesized patterns of directional and non-directional relationships among a set of observed (measured) and unobserved (latent) variables.
The structural equation consists of three latent variables and sixteen observed variables referred as linear, circular, and skinfold. The structural equation models (Byrne, 1998) are given below:
X1 = ξ1 + ε1
X2 = λ21 ξ1 + ε2
...........................
X6 = λ61 ξ1 + ε6
..........................
X8 = λ22 ξ2 + ε8
..........................
X17 = λ63 ξ3 + ε16
Where Xi (i=1 to 16) indicates observed variables, ξj (j= 1to 3) are latent variables, λij are the first order factor loading and εi indicates error variance.
Linear:ξ1 = γ1η + ζ1……………….………...(1)
Circular: ξ2 = γ2η + ζ2 …….…........…......….(2)
Skinfold: ξ3 = γ3η + ζ3………...........……….(3)
Where η is the endogenous (latent) variable (s), ξ indicates exogenous (latent) variable (s), γ1-γ3 are the coefficient of exogenous variables and ζ is any error among endogenous variables.
Now the structural equation model in vector form –
η = Γξ + ζ……………....……(4)
Causal Modelling or Path Analysis: Path analysis hypothesizes causal relationships among variables and tests the causal models with a linear equation system. Causal models can involve either manifest variables, latent variables, or both. SEM models are often illustrated in a path diagram. The path diagram is composed of boxes (each box represents one observed variable), ovals (each oval contains one latent variable), circles (represents the error of each observed and latent variable) and arrows (indicate paths connected with boxes and circles).
Confirmatory Factor Analysis (CFA): It is an extension of factor analysis where specific hypotheses about the structure of the factor loadings and inter-correlations are tested as to what extent the measured variables represent the number of constructs; and second-order confirmatory factor analysis, a variation of factor analysis in which the correlation matrix of the common factors is itself factor analysed to provide second order factors.
Variables
All anthropometric traits have been considered as manifest or observed (measurement) variables. Latent variables were not directly measured, but were determined simultaneously by first-order confirmatory factor analysis. It is represented by a set of manifest variables, which act as an indicator. SEM was performed using maximum likelihood estimation in statistical package AMOS, where linear, circular, skinfold and Composite Body Size Score (CBSS) are specified as latent variables.
Linear is the first latent component, comprising five anthropometric traits (Ht, Bad, Bid, Apc and Tvc). Circular is the second latent component, comprising five anthropometric traits (Ccn, Wc, Cc, Hipc and Muac). Skinfold is the third latent component, comprising six anthropometric traits (Skb, Skt, Sks, Ski, Ska and Skc). Finally, CBSS was constructed with the three latent components viz., linear, circular, and skinfold. The estimated CBSS scores were used in determining body size of the individuals. The second order CFA is the extension of first order CFA where the main construct determined the latent variables found in first order CFA 31.
Proposed Method for Optimal Cut off Points Based on CBSS
Two optimal cut off points were introduced for three types of body size, namely, lean body size, normal body size and robust body size based on the values of the CBSS.
Method
At first multiple linear regression analysis was performed using Weight (Wt) as a dependent variable and the rest of the anthropometric variables (measurement variables) as independent variables. The logic is to examine the contribution of each of the anthropometric traits to weight. Standardized predicted weight was estimated for each individual from the regression equation. Standardized weight could be positive or negative.
In the next step, I assessed the maximum standardized predicted weight (say, X) among the individuals and find its corresponding CBSS (say, Y). Hence Y is a first cut off point between robust and normal body size and was designated as the upper limit of normal body size or lower limit of robust body size. The lowest positive CBSS (say, Z) was designated as the lower limit of normal body size. Therefore, individuals having CBSS between a lower limit (Z) and upper limit (Y) were considered as normal body size score and those fell in this range (Z-Y) indicates the normal body size.
Individuals with positive CBSS and greater than the upper limit of normal CBSS (Y) were designated as robust body size.
Finally, individuals with negative CBSS i.e., < 0 (second cut off point) were categorized as lean body size.
Therefore, the study participants were categorized under Robust, Normal and Lean body sizes based on the following criteria (Figure 4).
Robust body size: Body size score > Y (positive value)
Normal body size: Body size score (Z – Y) (positive value)
Lean body size: Body size score < 0 (negative value)
Results
(Table 1) reveals the results of both first order and second order confirmatory factor analyses. This includes dependent variables, their path, latent variables with estimated unstandardized coefficients, standard errors, critical ratio, significant level and standardized coefficient. All the coefficients were highly significant. The standardized estimates allow for the evaluation of the relative contribution of each anthropometric trait to each latent variable. The result shows that for linear latent variable, transverse chest (Tvc) has the maximum factor loading of 0.89; for circular latent variable, chest circumference (Ccn) has the maximum factor loading of 0.87; and for skinfold latent variable, triceps skinfold (Skt) has the maximum factor loading of 0.92. The standard errors are estimates of the errors of unstandardized coefficients to be expected because of the sampling error.
Table 1. The Regression path coefficients of dependent variables on latent variables and its significance| Dependent Variables | Paths | Latent Variables | Estimated Coefficients | Standard Errors | Critical Ratio | Sig (P) | Standardized Coefficient |
| Ht | ← | Linear | 1.00 (reference point) | 0.825 | |||
| Bad | ← | Linear | 0.341 | 0.012 | 29.352 | ** | 0.847 |
| Bid | ← | Linear | 0.110 | 0.011 | 10.377 | ** | 0.444 |
| Apc | ← | Linear | 0.204 | 0.012 | 17.308 | ** | 0.747 |
| Tvc | ← | Linear | 0.274 | 0.013 | 21.620 | ** | 0.888 |
| Ccn | ← | Circular | 1.00 (reference point) | 0.870 | |||
| Wc | ← | Circular | 1.089 | 0.037 | 29.206 | ** | 0.804 |
| Hipc | ← | Circular | 0.855 | 0.033 | 26.077 | ** | 0.843 |
| Cc | ← | Circular | 0.296 | 0.018 | 16.148 | ** | 0.560 |
| Muac | ← | Circular | 0.367 | 0.014 | 25.323 | ** | 0.790 |
| Skb | ← | Skinfold | 1.00 (reference point) | 0.825 | |||
| Skt | ← | Skinfold | 2.476 | 0.081 | 30.689 | ** | 0.916 |
| Sks | ← | Skinfold | 2.292 | 0.095 | 24.030 | ** | 0.824 |
| Ski | ← | Skinfold | 2.085 | 0.095 | 20.462 | ** | 0.722 |
| Ska | ← | Skinfold | 2.419 | 0.1140 | 17.247 | ** | 0.639 |
| Skc | ← | Skinfold | 2.400 | 0.089 | 27.060 | ** | 0.860 |
| Linear | ← | Body Size | 1.00 (reference point) | 6.049 | |||
| Circular | ← | Body Size | 0.015 | 0.002 | 6.034 | ** | 0.132 |
| Skinfold | ← | Body Size | -0.002 | 0.001 | -5.513 | ** | -0.073 |
The first-order main sub-construct latent variables (linear and circular) have a significant loading with 6.05 and 0.13 respectively on second-order main constructs latent variable CBSS. These loading values show that linear latent variable has more influence in determining CBSS compared to other two latent variables. Table 1 further mentions the reference point 1.00 (standardized factor loading), which indicates fixing the variance of the corresponding variables within each group; thereby freely estimating the other concerning with the reference variable.
(Table 2) demonstrates the variance of the default model. The estimated variance explained for each of the measurement errors may be an observed or a latent variable associated with the measurement. The result shows that all the variances were highly significant.
Table 2. Estimated variances of each parameters in default model)| Estimate | S.E. | C.R. | P | Label | |
| e20 | 2026.868 | 330.186 | 6.139 | *** | par_61 |
| e1 | 1971.475 | 329.334 | 5.986 | *** | par_62 |
| e7 | 23.917 | 1.664 | 14.377 | *** | par_63 |
| e13 | 2.279 | .174 | 13.129 | *** | par_64 |
| e2 | 26.076 | 2.192 | 11.898 | *** | par_65 |
| e3 | 2.538 | .193 | 13.145 | *** | par_66 |
| e4 | 2.704 | .147 | 18.454 | *** | par_67 |
| e5 | 1.818 | .120 | 15.186 | *** | par_68 |
| e6 | 1.114 | .101 | 11.064 | *** | par_69 |
| e8 | 7.721 | .609 | 12.684 | *** | par_70 |
| e9 | 1.977 | .127 | 15.568 | *** | par_71 |
| e10 | 15.829 | 1.110 | 14.257 | *** | par_72 |
| e11 | 7.243 | .550 | 13.179 | *** | par_73 |
| e12 | 2.929 | .201 | 14.585 | *** | par_74 |
| e14 | 1.074 | .073 | 14.611 | *** | par_75 |
| e15 | 2.680 | .250 | 10.739 | *** | par_76 |
| e16 | 5.763 | .385 | 14.978 | *** | par_77 |
| e17 | 9.148 | .556 | 16.453 | *** | par_78 |
| e18 | 19.475 | 1.118 | 17.418 | *** | par_79 |
| e19 | 4.629 | .337 | 13.722 | *** | par_80 |
(Table 3) represents the fit indices to evaluate the goodness of the model. SEM was used for modification indices to meet the accuracy and precision of structured prediction equations since the fit of the model was not adequate.
Table 3. Summary of Model Fit Indices| Fit Index | Values |
| Likelyhood Ratio (Chi2), Df = 72 | 1006.22** |
| CMIN/Df | 13.97 |
| Akaike,s Information Criteria (AIC) | 1166.22 |
| Bayesian Information Criteria (BIC) | 1170.15 |
| Comparative Fit Index (CFI) | 0.91 |
| Tucker-Lewis Index (TLI) | 0.85 |
| NFI | 0.90 |
| IFI | 0.91 |
| Root Mean Square Error of Approximation (RMSEA) | 0.13 |
The Maximum Likelihood Estimation method is widely used to maximize the fit of the model and also to estimate all model parameters simultaneously. Modification of the model is the general procedure to improve the fit. In this model, I applied the modification indices to maintain the correlation- covariance between the measurement errors derived from the model that provided maximum improvement in fit and the process was continued until to reach an adequate fit. The determination of model fit in SEM technique produce Chi-square statistic which is the test of absolute fit of the model and the Chi-square value should reach p > 0.05. From the modified model, result shows that the overall model fitting was highly significant (likelihood ratio, χ2= 1006.22, p ≤ 0.01) and do not allow for the consistent estimation of parameters in the model involving latent variables. However, 32 has mentioned that the Chi-square statistic is too sensitive to the large size of the sample for it to be interpreted as a significant test. Therefore, the Chi-square statistics was not used as a fit index for this study. Instead, we have turned to other relative fit indices that are comparatively less sensitive to large data set. Therefore, we used modern approaches in relative fit indices such as Comparative Fit Index (CFI), Tucker-Lewis Index (TLI) and Root Mean Square Error of Application (RMSEA) to fit the model. The values of these relative fit indices for the final model are found to be 0.91 (Comparative Fit Index), 0.85 (Tucker-Lewis Index), and 0.19 (Root Mean Square Error of Application). The values were close to the specified ranges 33, 34 which indicates that the higher-order three factors model provided a moderate fit to the data.
The fit indices expressed as the χ2, CMIN/DF, Akaike’s Information Criteria (AIC), Bayesian Information Criteria (BIC ), Comparative Fit Index (CFI), Tucker-Lewis Index (TLI) and Root Mean Square Error of Application ( RMSEA) values were as 1006.22 (p<0.01), 13.97, 1166.22, 1170.15, 0.91, 0.85 and 0.13 respectively.
(Figure 1) shows the standardized visual diagrams of second-order confirmatory factor analysis as well as of structural equation model (SEM). The figure consists of four latent variables- linear, circular and skinfold, and composite body size score, each representing different executive functions. The first three latent variables were measured using sixteen anthropometric traits derived from the first order confirmatory factor analysis. Later CBSS was estimated by the first three latent components derived from second-order confirmatory factor analysis. The figure represents the CBSS as the main construct (called second-order) while linear, circular, and skinfold are three sub-constructs (called first-order). The single-headed arrows that originate from the latent components (first-order) and terminate in the measured variable represent direct relationships from the latent variable to the measurement variables. In second-order confirmatory factor analysis, three arrows originated from the latent variable CBSS and terminated in the first-order three latent variables. In the figures, values shown from bottom to top are error variances (besides error), first-order factor loadings (beside arrows), and error variances of the first-order factor (in the circle), second-order factor loadings (beside arrows) respectively.
Figure 1.The composite indicators of the body size score with measurements and latent variables by second order confirmatory factor analysis (unstandardized)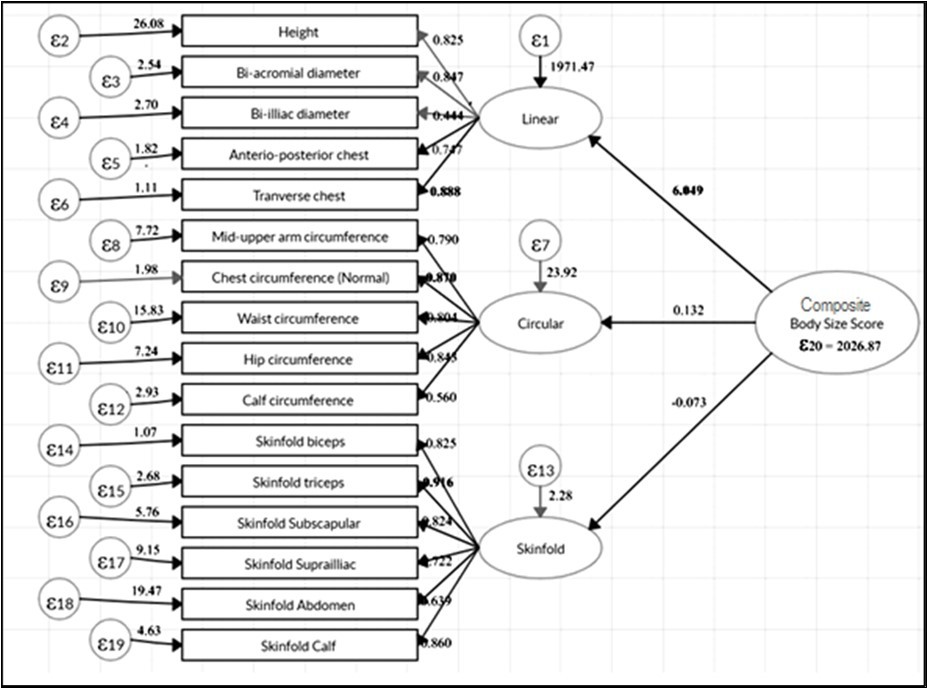
(Figure 2) represents the scatter plot on CBSS with standardized weight (measurement variable), where X- axis represents the standardized weight and Y-axis is the CBSS. The line in the scatter plot based on the origin of CBSS indicates a cut-off line (first cut off point). Individuals having scores below the line are either of normal or robust body size. In the scatter plot, at the top of the right corner, at location ‘A’ is the second cut-off point between normal and robust body size. The coordinate of location ‘A’ is (2.88, 3.09) indicates intercepts of maximum predicted standardized weight and corresponding CBSS. Hence, the area of the scatter plot is divided into three parts, the scores that fall in the area of the upper part represent robust body size, and those in the middle part represents normal body size and those in the lower part represents lean body size for this study population.
Figure 2.Classification of different Body Size categories by standardized body weight and body size score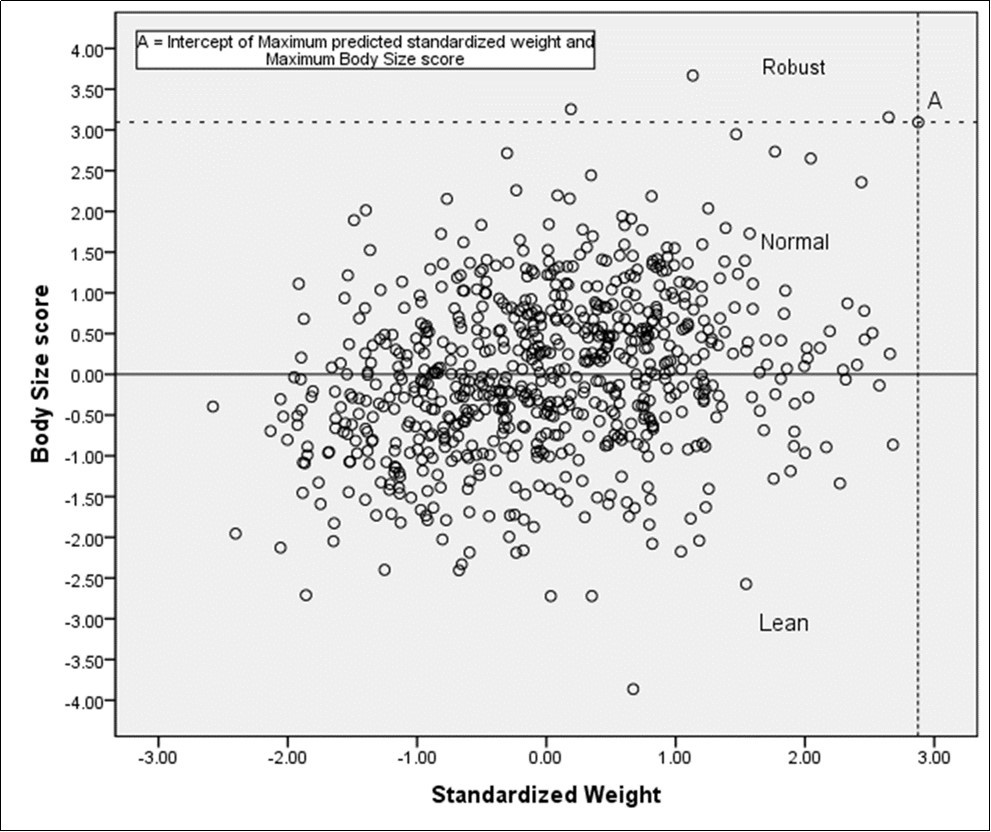
Based on the cut off points of CBSS, initially, the highest standardized weight (2.88) among the individuals and its corresponding CBSS (3.09) were noted. This value of CBSS (3.09) was designated as the upper limit of normal body size. The lowest positive CBSS (0.001) remained the lower limit of normal body size score. Individuals with CBSS greater than the upper limit of normal body size score (3.09) was considered as robust body size scores and those having CBSS values below 0.001 were considered with lean body size.
On the basis of the proposed cut-off points of CBSS, it has been found that 50.6%, 48.8% and 0.6% of the study participants fell respectively in lean, normal and robust body size categories. It is remarkable that females frequently exhibit lean body size (73.8%) compared to the males (26.2%) in the population as only lean body size scores are take into consideration. Furthermore, result indicates that female participants are more under nutrition than male.
(Figure 3) also reveals the scatter plot on CBSS with age, where X- axis represents the CBSS and Y-axis the age. Since the plotting points were spread all over the plot areas, it indicates that the two variables were independent fitted lines. The figure further reveals that the values of R2 were near to zero on both sexes, indicating that the sex is independent of CBSS.
Figure 3.Age and Sex-wise scatter plot on body size scores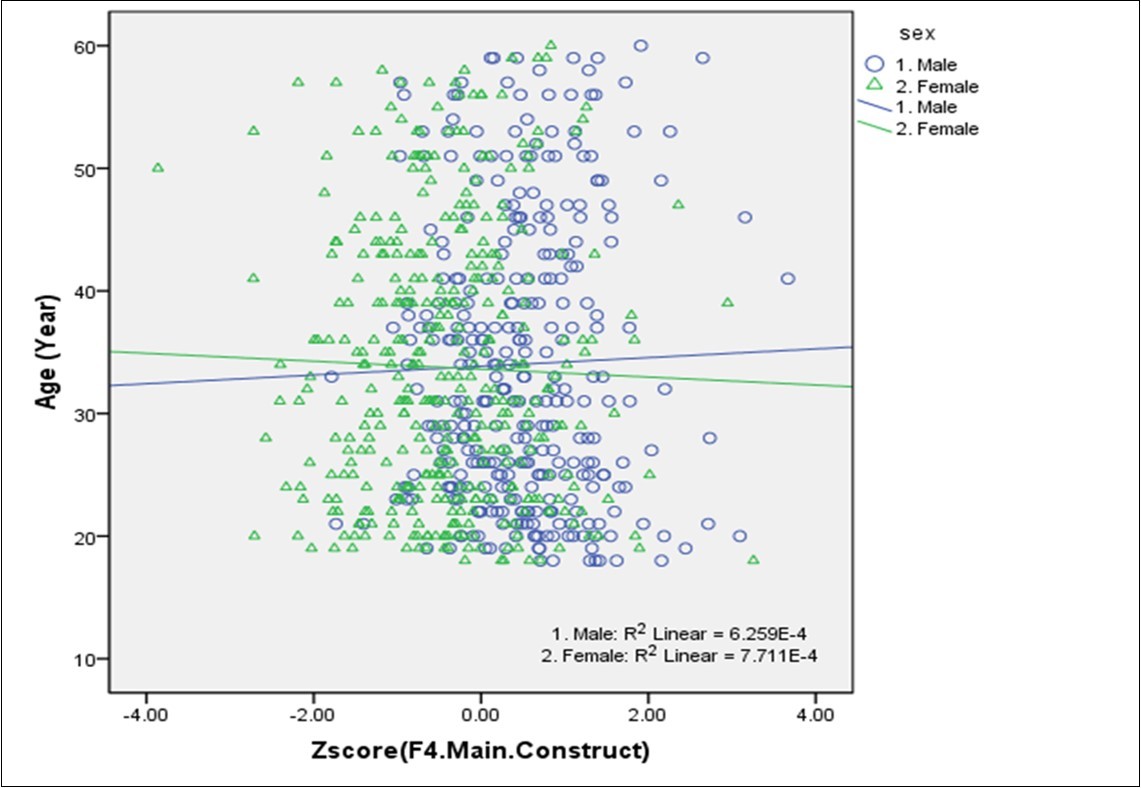
(Figure 4) represents the bar diagram of mean values of all anthropometric traits separately on three types of body size. It appears from the figures that means of all traits of the linear and circular and skinfold components are high to robust body size, followed by normal and lean body sizes.
Figure 4.Mean values of anthropometric measurements in different groups of 'Body Size'
Discussion
Since CBSS is independent of age and sex (shown in Figure 3) it can be considered as a unique method to classify the distinct body size in any population. The accuracy of the classification of body size using this statistical model may be considered better and satisfactory due to the consideration of a number of anthropometric traits in the analysis 8. As a result, the higher order three-factor model was preferred for determining body size. As a general assumption, results focused on mean values of most of the measurement variables maintained increasing higher order from Lean body size to robust body size is the validity of the model.
The high value of coefficient of several anthropometric traits such as, transverse chest (Tvc), chest circumference (Ccn), skinfold triceps (Skt) reflects the high contribution of these respective latent component in the first order model. and the latent component linear was found to have contributed the most in second-order model.
Thus, the derived statistical model suggests that anthropometric traits can be used to determine the CBSS based on the hypothesis of the study.
Conclusion
It may be concluded that the proposed models may be used as a precise estimator to assess the body size of a population and in determining the nutritional status. The advantages of this method lie in terms of assessment of body size are: reliability and feasibility and cost effectiveness.
Limitations
The model would have been more précised with the increase in sample size. The method is generalized concerning the cut-off points of different categories of body size but may remain inconsistence across populations. An adequate number of community-based studies can give better insights into population variation in body size cut-off values.
Acknowledgment
The author is indebted to the study participants for their unhesitating involvement and to the authority of the Indian Statistical Institute for providing financial support for this research. The author is also immensely grateful to Prof. Subha Roy and Dr. Indrajit Dasgupta for their valuable comments and throughout editing the manuscript. Thanks to Mr. Akash Mallick for his technical support and revision of the manuscript. Prof. Barun Mukhopadhyay and Prof. Chrales Weitz, are also acknowledged for the crucial grammatical revisions and suggestions.
Availability of Data and Material
The dataset used and/or analysed during the current study are available from the author on reasonable request.
Author’s Contributions
The Author solely contributed to the set design, data analysis and interpretation of the results as well as preparing the drafts of the manuscript.
References
- 1.A M Neville, Bate S, R L Holder. (2005) Modeling Physiological and Anthropometric variables known to vary with body size and other confounding variables.Yearbook of Physical Anthropology. 18, 141-153.
- 2.M P Reed, Raschke U, Tirumali R, M B Parkinson. (2014) Developing and Implementing Parametric Human Body Shape Models in Ergonomics Software. Parametric Human Body Models. in Ergonomics Software,International Digital Human Modeling Conference, 3rd, Tokyo,Japan 1-8.
- 3.Lacko D, Huysmans T, P M, G D Bruyne, Verwulgen S et al. (2015) Evaluation of an anthropometric shape model of the human scalp.Applied. , Regonomics 48, 70-85.
- 4.Sheldon W H, Stevens S S, Tucker W B. (1941) . , The Varieties of Human Physique.American Anthropologist 43, 470-474.
- 5.Y S Kusuma, V B Babu, J M Naidu. (2008) Chronic energy deficiency in some low socio-economic population from South India: Relationship between Body Mass Index, Waist-hip ratio and Conicity index.Homo. 59(1), 67-79.
- 6.V Cornelissen Groves, McCarty P, Mohamed K, Maalin S, Tovée N et al. (2019) . How Does Variation in the Body Composition of Both Stimuli and Participant Modulate Self-Estimates of Men’s Body Size?Front. Psychiatry,09 https://doi.org/10.3389/fpsyt.2019.00720 .
- 7.B N Pal, Seal B, S K Roy. (2014) Nutritional Status of Fishermen Communities: validation of conventional methods with discriminant function analysis.Bulletin of. , Mathematical Sciences & Applications 8, 49-59.
- 8.Bhattacharya A, B N Pal, Mukherjee S, S K Roy. (2019) Assessment of nutritional status using anthropometric variables by multivariate analysis.BMC:. , Public Health 9, 1-9.
- 9.N M Laird, J H Ware. (1982) Random-effects models for longitudinal data.Journal of. , American College Health 31, 105-108.
- 10.Takada K, A, V K Freund. (1984) Canonical correlations between masticatory muscle orientation and dentoskeletal morphology in children. , AmericanJournal of Orthodontics 86, 331-41.
- 11.Goldstein H. (1986) Effect on statistical modelling of longitudinal data.Annals. , of Human Biology 13, 129-141.
- 12.Goldstein H. (1989) Flexible models for the analysis of growth data with an application to height prediction.Revue Epidemiol Sante Publique. 37, 477-484.
- 13.W H Mueller, Marbella A, R B Harrist, H J Kaplowitz, J A Grunbaum et al. (1989) Body circumferences as alternatives to skinfold measures of body fat distribution in children.Annals of Human Biology,16,495-506.
- 14.W H Mueller, M L Wear, C L Hanis, J B Emerson, S A Barton et al. (1991) Which measurement of body fat distribution is best for epidemiologic research?. , AmericanJournal of Epidemiology,133 858-869.
- 15.S O Ismaila, O G Akanbi, C N Ngassa. (2014) Models for estimating the anthropometric dimension using standard height for furniture design.Journal of Engineering Design and. 12(3), 336-347.
- 16.P C Mahanalanobis. (1930) On tests and measures of group divergence.Journal of the Asiatic Society. 26-541.
- 17.P C Mahalanobis. (1936) On the generalized distance in statistics.Proc. , NatlInst Sci India 2, 49-55.
- 18.C R Rao. (1946) On the linear combination of observations and the general theory of least square.Sankhya. 7, 237-256.
- 19.C R Rao. (1947) The problem of classification and distance between two populations.Nature. 159, 30-31.
- 21.Kapoor S, Kapoor A. (2005) Body structure and respiratory efficiency among high altitude Himalayan populations.Collegium. , Anthropology 29, 37-43.
- 22.Tripathy V, Gupta R. (2007) Blood Pressure variation among Tibetans at different altitudes.Annals of Human. , Biology 34, 470-483.
- 23.C J Anitha, M K Nair, Rajamohanan K, S M Nair, K T Shenoy et al. (2009) Predictors of birth weight-a cross sectional study.Indian. , Pediatrics 46, 56-62.
- 24.Singh J, R K Pathak, K H Chavali. (2011) Skeletal height estimation from regression analysis of sterna lengths in a Northwest Indian population of Chandigarh region: a post-mortem study.Forensic. , Science International 206, 211-8.
- 25.S J Benjamin, A B Danial, Kamath A, Ramkumar V. (2012) Anthropometric measurements as predictors of cephalopelvic disproportion: Can the diagnostic accuracy be improved?Acta Obstet Gynecol Scandinavic. 91, 122-127.
- 26.B N Pal, Seal B. (2011) Bias estimation of regression parameters using Jack-knife resampling technique in populations of two geographically contrasting regions.International. , Journal of Statistics and Analysis 1, 405-418.
- 28.Hoyle R H. (1995) The structural equation modeling approach: Basic concepts and fundamental issues. In Structural equation modeling: Concepts issues, and applications, R. H. Hoyle (editor) 1-15.
- 29.E. (1998) Structural equation modeling.In Modern methods for business. research, G.A. Marcoulides (editor). Mahwah, NJ: Lawrence Erlbaum Associates 251-294.
- 30.R C MacCallum, J T Austin. (2000) Applications of structural equation modeling in psychological research.Annual Review of. , Psychology 51, 201-226.
- 31.D F Rindskopf, Rose T. (1988) Some theory and applications of confirmatory second-order factor analysis.Multivariate. , Behavioural Research 23, 51-67.
